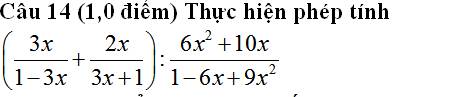\(đk:\left\{{}\begin{matrix}x\ne-\dfrac{1}{3}\\x\ne\dfrac{1}{3}\end{matrix}\right.\)
\(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\left(\dfrac{6x^2+10x}{1-6x+9x^2}\right)\\ =\left(\dfrac{3x\left(3x+1\right)+2x\left(1-3x\right)}{1-9x^2}\right)\times\left(\dfrac{\left(1-3x\right)^2}{6x^2+10x}\right)\\ =\left(\dfrac{9x^2+3x+2x-6x^2}{1-9x^2}\right)\times\left(\dfrac{\left(1-3x\right)^2}{2x\left(3x+5\right)}\right)\\ =\left(\dfrac{3x^2+5x}{\left(1-3x\right)\left(1+3x\right)}\right)\times\left(\dfrac{\left(1-3x\right)^2}{2\left(3x^2+5x\right)}\right)\\ =\dfrac{1-3x}{2.\left(1+3x\right)}\)
Đúng 2
Bình luận (0)
