Bài 1
a) 5(x - 3) + 5 = 4x + 1
5x - 15 + 5 = 4x + 1
5x - 4x = 1 + 15 - 5
x = 11
Vậy S = {11}
b) (x - 2)/6 - x/2 = (5 - 2x)/3
x - 2 - 3x = 2(5 - 2x)
-2x - 2 = 10 - 4x
-2x + 4x = 10 + 2
2x = 12
x = 12 : 2
x = 6
Vậy S = {6}
Bài 2
a) Có hai khả năng rút được thẻ có ghi số có chữ số tận cùng là 2 là: 2 và 12
⇒ P = 2/20 = 1/10
b) Có 1 khả năng rút được thẻ có hai chữ số mà tích của hai chữ số là 4 là số: 14
⇒ P = 1/20
Bài 3 thiếu dữ liệu độ dài quãng đường AB nên không giải được
Bài 4
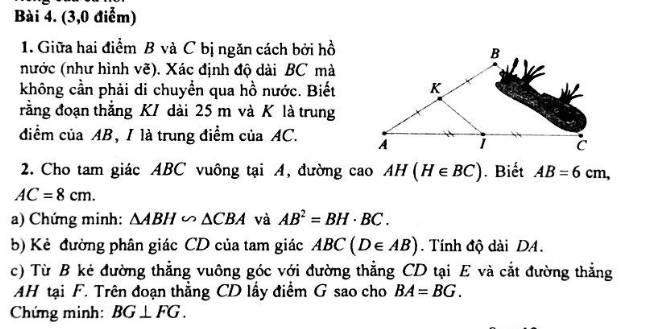
1)
Do K là trung điểm của AB (gt)
I là trung điểm của AC (gt)
⇒ KI là đường trung bình của ∆ABC
⇒ KI = BC : 2
⇒ BC = 2KI = 2.25 = 50 (m)
Bài 4
2)
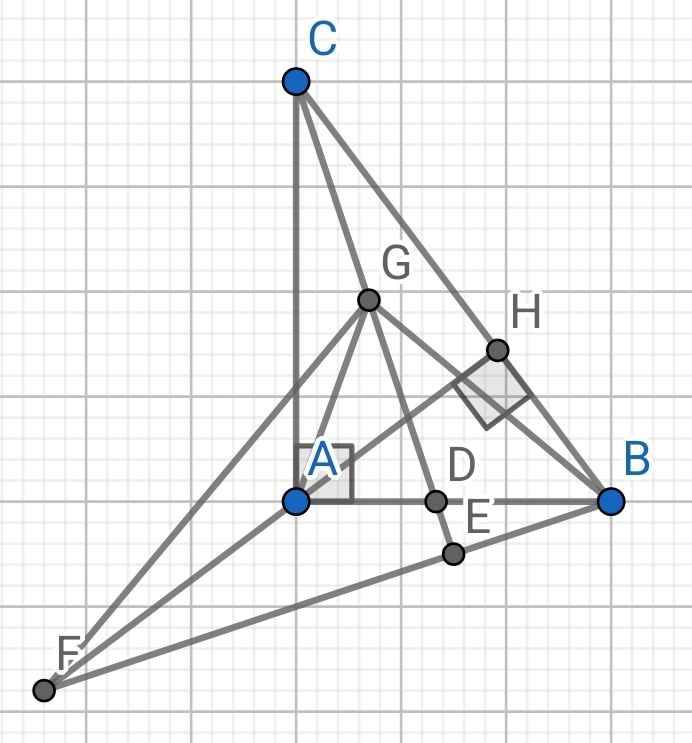
a) Xét hai tam giác vuông: ∆ABH và ∆CBA có:
∠B chung
⇒ ∆ABH ∽ ∆CBA (g-g)
⇒ AB/BC = BH/AB
⇒ AB² = BH.BC
b) ∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pythagore)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là đường phân giác của ∆ABC (gt)
⇒ DA/DB = CA/CB
⇒ DA/CA = DB/CB
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
DA/CA = DB/CB = (DA + DB)/(CA + CB) = AB/(8 + 10) = 6/18 = 1/3
DA/CA = 1/3
⇒ DA = 1/3 . CA
= 8/3 (cm)
c) Ta có:
AB² = BH.BC (cmt)
Mà BA = BG (gt)
⇒ BG² = BH.BC (1)
Xét hai tam giác vuông: ∆EBC và ∆HBF có:
∠B chung
⇒ ∆EBC ∽ ∆HBF (g-g)
⇒ BC/BF = BE/BH
⇒ BH.BC = BE.BF (2)
Từ (1) và (2) ⇒ BG² = BE.BF
⇒ BG/BE = BF/BG
Xét ∆BGF và ∆BEG có:
BG/BE = BF/BG (cmt)
∠B chung
⇒ ∆BGF ∽ ∆BEG (c-g-c)
⇒ ∠BGF = ∠BEG = 90⁰
⇒ BG ⊥ FG