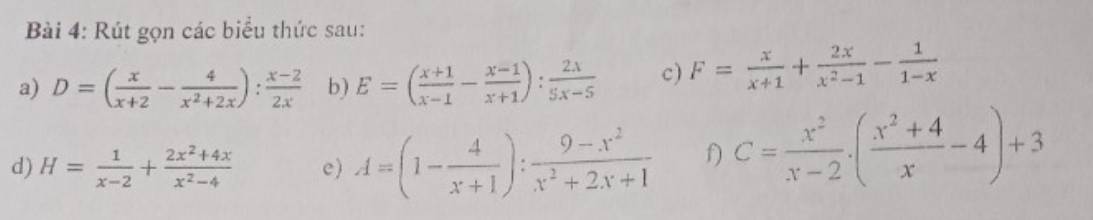a: ĐKXĐ: \(x\notin\left\{2;0;-2\right\}\)
\(D=\left(\dfrac{x}{x+2}-\dfrac{4}{x^2+2x}\right):\dfrac{x-2}{2x}\)
\(=\left(\dfrac{x}{x+2}-\dfrac{4}{x\left(x+2\right)}\right)\cdot\dfrac{2x}{x-2}\)
\(=\dfrac{x^2-4}{x\left(x+2\right)}\cdot\dfrac{2x}{\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)\cdot2}{\left(x+2\right)\left(x-2\right)}=2\)
b: ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)
\(E=\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{5\left(x-1\right)}{2x}\)
\(=\dfrac{x^2+2x+1-x^2+2x-1}{\left(x+1\right)}\cdot\dfrac{5}{2x}\)
\(=\dfrac{4x\cdot5}{2x\left(x+1\right)}=\dfrac{10}{x+1}\)
c: ĐKXĐ:\(x\notin\left\{1;-1\right\}\)
\(F=\dfrac{x}{x+1}+\dfrac{2x}{x^2-1}-\dfrac{1}{1-x}\)
\(=\dfrac{x}{x+1}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}+\dfrac{1}{x-1}\)
\(=\dfrac{x\left(x-1\right)+2x+x+1}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{x^2-x+3x+1}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2+2x+1}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(x-1\right)}=\dfrac{x+1}{x-1}\)
d: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(H=\dfrac{1}{x-2}+\dfrac{2x^2+4x}{x^2-4}\)
\(=\dfrac{1}{x-2}+\dfrac{2x\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{1}{x-2}+\dfrac{2x}{x-2}=\dfrac{2x+1}{x-2}\)
e: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
\(A=\left(1-\dfrac{4}{x+1}\right):\dfrac{9-x^2}{x^2+2x+1}\)
\(=\dfrac{x+1-4}{x+1}\cdot\dfrac{\left(x+1\right)^2}{-\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x-3}{1}\cdot\dfrac{x+1}{-\left(x+3\right)\left(x-3\right)}=\dfrac{-\left(x+1\right)}{x+3}\)
f: ĐKXĐ: \(x\notin\left\{0;2\right\}\)
\(C=\dfrac{x^2}{x-2}\cdot\left(\dfrac{x^2+4}{x}-4\right)+3\)
\(=\dfrac{x^2}{x-2}\cdot\dfrac{x^2+4-4x}{x}+3\)
\(=\dfrac{x^2}{x}\cdot\dfrac{\left(x-2\right)^2}{x-2}+3\)
\(=x\left(x-2\right)+3=x^2-2x+3\)