Câu 15:
Gọi vận tốc theo dự định của người đó là \(x(km/h;x>0)\)
Vận tốc trên thực tế của người đó là: \(x-5(km/h)\)
Thời gian người đó đi quãng đường AB theo dự định là:
11 giờ 30 phút - 7 giờ = 4 giờ 30 phút = 4,5 giờ
Thời gian người đó đi quãng đường AB trên thực tế là:
12 giờ - 7 giờ = 5 giờ
Khi đó ta có pt để tính quãng đường AB là: \(4,5x=5\left(x-5\right)\)
\(\Leftrightarrow5x-25=4,5x\)
\(\Leftrightarrow0,5x=25\)
\(\Leftrightarrow x=50\) (tmđk)
Độ dài quãng đường AB là: \(50\cdot4,5=225\left(km\right)\)
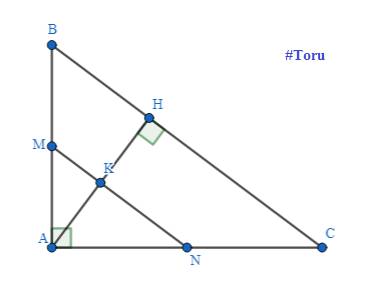
Câu 16:
a) Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{CAB}\left(AH\perp BC;\Delta ABC\text{ vuông tại }A\right)\\\widehat{ABC}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow \Delta HBA \backsim \Delta ABC(g.g)\)
b) Xét \(\Delta ABC\) vuông tại A có: \(BC^2=AB^2+AC^2\) (đlí Pythagore)
\(\Rightarrow BC^2=3^2+4^2=25\)
\(\Rightarrow BC=\sqrt{25}=5\) (cm) (vì BC > 0)
Vì \(\Delta HBA\backsim\Delta ABC(cmt)\Rightarrow \dfrac{AB}{CB}=\dfrac{HB}{AB}\) (các cạnh t/ứng)
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Khi đó: \(HC+BH=BC\) (do \(H\in BC\))
\(\Rightarrow HC=BC-BH=5-1,8=3,2\left(cm\right)\)
c) Xét \(\Delta AHB\) vuông tại H có: \(AB^2=AH^2+BH^2\) (đlí Pythagore)
\(\Rightarrow AH^2=AB^2-BH^2=3^2-1,8^2=5,76\)
\(\Rightarrow AH=\sqrt{5,76}=2,4\left(cm\right)\) (vì AH > 0)
Khi đó: \(\dfrac{AK}{AH}=\dfrac{1,2}{2,4}=\dfrac{1}{2}\Rightarrow AH=2AK\)
\(\Rightarrow K\) là trung điểm \(AH\) (do \(K\in AH\)) \(\Rightarrow KH=AK=1,2\left(cm\right)\)
Xét \(\Delta AHC\) có: \(\begin{cases} K\text{ là trung điểm } AH\text{ (cmt) }\\ KN//HC\text{ ( KN//BC };H\in BC) \end{cases} \)
\(\Rightarrow N\) là trung điểm của \(AC\) (t/c)
Xét \(\Delta ABC\) có: \(\begin{cases} MN//BC(gt)\\ N\text{ là trung điểm }AC(cmt) \end{cases} \)
\(\Rightarrow M\) là trung điểm của \(AB\) (t/c)
\(\Rightarrow MN\) là đường trung bình của \(\Delta ABC\Rightarrow MN=\dfrac{BC}{2}=\dfrac{5}{2}=2,5\left(cm\right)\)
Vì \(MN//BC\Rightarrow BMNC\) là hình thang
Xét hình thang \(BMNC(MN//BC)\) có: \(KH\perp BC\)
\(\Rightarrow S_{BMNC}=\dfrac{1}{2}\cdot\left(MN+BC\right)\cdot KH=\dfrac{1}{2}\cdot\left(2,5+5\right)\cdot1,2=4,5\left(cm^2\right)\)
\(\text{#}Toru\)