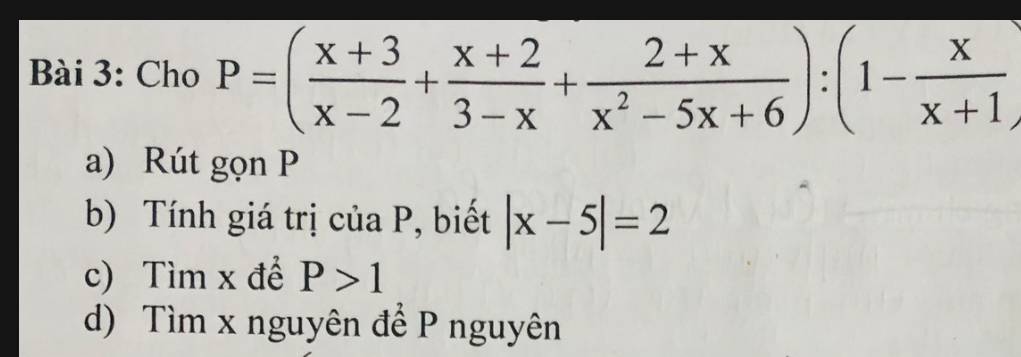a: ĐKXĐ: \(x\notin\left\{2;3;-1\right\}\)
\(P=\left(\dfrac{x+3}{x-2}+\dfrac{x+2}{3-x}+\dfrac{2+x}{x^2-5x+6}\right):\left(1-\dfrac{x}{x+1}\right)\)
\(=\left(\dfrac{x+3}{x-2}-\dfrac{x+2}{x-3}+\dfrac{x+2}{\left(x-2\right)\left(x-3\right)}\right):\dfrac{x+1-x}{x+1}\)
\(=\dfrac{\left(x+3\right)\left(x-3\right)-\left(x-2\right)\left(x+2\right)+x+2}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x+1}{1}\)
\(=\dfrac{x^2-9-x^2+4+x+2}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x+1}{1}\)
\(=\dfrac{x-3}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x+1}{1}=\dfrac{x+1}{x-2}\)
b: |x-5|=2
=>\(\left[{}\begin{matrix}x-5=2\\x-5=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=3\left(loại\right)\end{matrix}\right.\)
Khi x=7 thì \(P=\dfrac{7+1}{7-2}=\dfrac{8}{5}\)
c: P>1
=>P-1>0
=>\(\dfrac{x+1-x+2}{x-2}>0\)
=>\(\dfrac{3}{x-2}>0\)
=>x-2>0
=>x>2
d: Để P nguyên thì \(x+1⋮x-2\)
=>\(x-2+3⋮x-2\)
=>\(3⋮x-2\)
=>\(x-2\in\left\{1;-1;3;-3\right\}\)
=>\(x\in\left\{3;1;5;-1\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{1;5\right\}\)