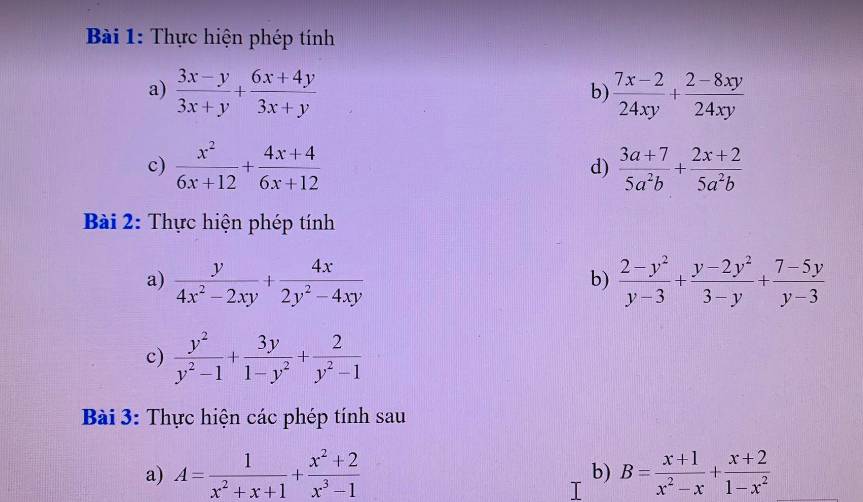Bài 1
a) \(\dfrac{3x-y}{3x+y}+\dfrac{6x+4y}{3x+y}\)
\(=\dfrac{3x-y+6x+4y}{3x+y}\)
\(=\dfrac{9x+3y}{3x+y}\)
\(=\dfrac{3\left(3x+y\right)}{3x+y}\)
\(=3\)
b) \(\dfrac{7x-2}{24xy}+\dfrac{2-8xy}{24xy}\)
\(=\dfrac{7x-2+2-8xy}{24xy}\)
\(=\dfrac{7x-8xy}{24xy}\)
\(=\dfrac{x\left(7-8y\right)}{24xy}\)
\(=\dfrac{7-8y}{24y}\)
c) \(\dfrac{x^2}{6x+12}+\dfrac{4x+4}{6x+12}\)
\(=\dfrac{x^2+4x+x}{6x+12}\)
\(=\dfrac{\left(x+2\right)^2}{6\left(x+2\right)}=\dfrac{x+2}{6}\)
d) \(\dfrac{3a+7}{5a^2b}+\dfrac{2x+2}{5a^2b}\)
\(=\dfrac{3a+7+2x+2}{5a^2b}\)
\(=\dfrac{3a+2x+9}{5a^2b}\)
Bài 2
a) \(\dfrac{y}{4x^2-2xy}+\dfrac{4x}{2y^2-4xy}\)
\(=\dfrac{y}{2x\left(2x-y\right)}-\dfrac{4x}{2y\left(2x-y\right)}\)
\(=\dfrac{y^2}{2xy\left(2x-y\right)}-\dfrac{4x^2}{2xy\left(2x-y\right)}\)
\(=\dfrac{y^2-4x^2}{2xy\left(2x-y\right)}\)
\(=\dfrac{\left(y-2x\right)\left(y+2x\right)}{2xy\left(2x-y\right)}\)
\(=\dfrac{-2x-y}{2xy}\)
b) \(\dfrac{2-y^2}{y-3}+\dfrac{y-2y^2}{3-y}+\dfrac{7-5y}{y-3}\)
\(=\dfrac{2-y^2}{y-3}-\dfrac{y-2y^2}{y-3}+\dfrac{7-5y}{y-3}\)
\(=\dfrac{2-y^2-y+2y^2+7-5y}{y-3}\)
\(=\dfrac{y^2-6y+9}{y-3}\)
\(=\dfrac{\left(y-3\right)^2}{y-3}\)
\(=y-3\)
c) \(\dfrac{y^2}{y^2-1}+\dfrac{3y}{1-y^2}+\dfrac{2}{y^2-1}\)
\(=\dfrac{y^2}{y^2-1}-\dfrac{3y}{y^2-1}+\dfrac{2}{y^2-1}\)
\(=\dfrac{y^2-3y+2}{y^2-1}\)
\(=\dfrac{y^2-2y-y+2}{\left(y-1\right)\left(y+1\right)}\)
\(=\dfrac{\left(y^2-2y\right)-\left(y-2\right)}{\left(y-1\right)\left(y+1\right)}\)
\(=\dfrac{y\left(y-2\right)-\left(y-2\right)}{\left(y-1\right)\left(y+1\right)}\)
\(=\dfrac{\left(y-2\right)\left(y-1\right)}{\left(y-1\right)\left(y+1\right)}\)\
\(=\dfrac{y-2}{y+1}\)
Bài 3
a) \(A=\dfrac{1}{x^2+x+1}+\dfrac{x^2+2}{x^3-1}\)
\(=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x-1+x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x-1}\)
b) \(B=\dfrac{x+1}{x^2-x}+\dfrac{x+2}{1-x^2}\)
\(=\dfrac{x+1}{x\left(x-1\right)}-\dfrac{x+2}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x+1\right)^2-x\left(x+2\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x^2+2x+1-x^2-2x}{x\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{1}{x\left(x-1\right)\left(x+1\right)}\)