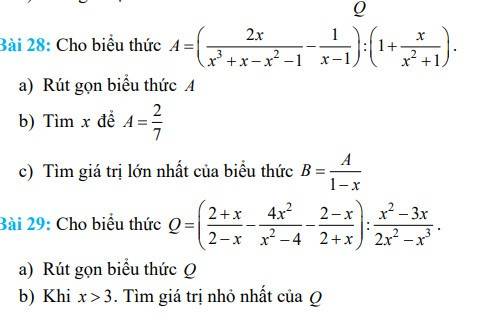Bài 29:
a: ĐKXĐ: \(x\notin\left\{2;-2;0;3\right\}\)
\(Q=\left(\dfrac{2+x}{2-x}-\dfrac{4x^2}{x^2-4}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-3x}{2x^2-x^3}\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right):\dfrac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{x+2}\cdot\dfrac{-x}{x-3}\)
\(=\dfrac{-4x^2-8x}{x+2}\cdot\dfrac{-x}{x-3}\)
\(=\dfrac{4x\left(x+2\right)}{x+2}\cdot\dfrac{x}{x-3}=\dfrac{4x^2}{x-3}\)
b: \(Q=\dfrac{4x^2}{x-3}\)
\(=\dfrac{4x^2}{x-3}-48+48\)
\(=\dfrac{4x^2-48x+144}{x-3}+48\)
\(=\dfrac{4\left(x^2-12x+36\right)}{x-3}+48\)
\(=\dfrac{4\left(x-6\right)^2}{x-3}+48>=48\forall x>3\)
Dấu '=' xảy ra khi x-6=0
=>x=6(nhận)
Bài 28:ĐKXĐ: x<>1
a: \(A=\left(\dfrac{2x}{x^3-x^2+x-1}-\dfrac{1}{x-1}\right):\left(1+\dfrac{x}{x^2+1}\right)\)
\(=\left(\dfrac{2x}{\left(x-1\right)\left(x^2+1\right)}-\dfrac{1}{x-1}\right):\dfrac{x^2+x+1}{x^2+1}\)
\(=\dfrac{2x-x^2-1}{\left(x-1\right)\left(x^2+1\right)}\cdot\dfrac{x^2+1}{x^2+x+1}\)
\(=\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{-x+1}{x^2+x+1}\)
b: \(A=\dfrac{2}{7}\)
=>\(\dfrac{-x+1}{x^2+x+1}=\dfrac{2}{7}\)
=>\(2\left(x^2+x+1\right)=7\left(-x+1\right)\)
=>\(2x^2+2x+2+7x-7=0\)
=>\(2x^2+9x-5=0\)
=>\(2x^2+10x-x-5=0\)
=>(x+5)(2x-1)=0
=>\(\left[{}\begin{matrix}x=-5\left(nhận\right)\\x=\dfrac{1}{2}\left(nhận\right)\end{matrix}\right.\)
c: \(B=\dfrac{A}{1-x}=\dfrac{1-x}{x^2+x+1}:\left(1-x\right)=\dfrac{1}{x^2+x+1}\)
\(=\dfrac{1}{x^2+x+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{1}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}< =1:\dfrac{3}{4}=\dfrac{4}{3}\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)