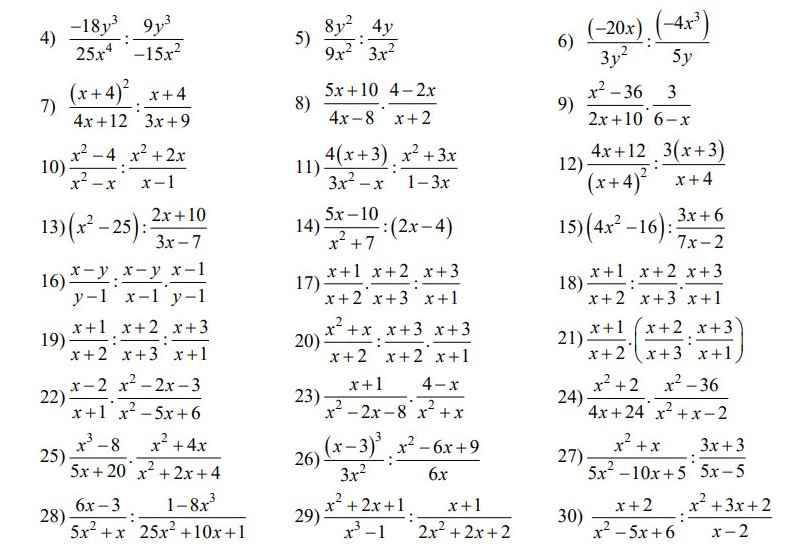4.
$\frac{-18y^3}{25x^4}: \frac{9y^3}{-15x^2}=\frac{-18y^3}{25x^4}.\frac{-15x^2}{9y^3}=\frac{-18y^3}{9y^3}.\frac{-15x^2}{25x^4}$
$=-2.\frac{-3}{5x^2}=\frac{6}{5x^2}$
5.
$\frac{8y^2}{9x^2}:\frac{4y}{3x^2}=\frac{8y^2}{9x^2}.\frac{3x^2}{4y}$
$=\frac{8y^2}{4y}.\frac{3x^2}{9x^2}$
$=2y.\frac{1}{3}=\frac{2y}{3}$
8.
$\frac{5x+10}{4x-8}.\frac{4-2x}{x+2}=\frac{5(x+2)}{4(x-2)}.\frac{-2(x-2)}{x+2}$
$=\frac{5(x+2)}{x+2}.\frac{-2(x-2)}{4(x-2)}=5.\frac{-1}{2}=\frac{-5}{2}$
9.
$\frac{x^2-36}{2x+10}.\frac{3}{6-x}=\frac{(x-6)(x+6)}{2x+10}.\frac{-3}{x-6}$
$=\frac{-3(x+6)}{2x+10}$
6.
$\frac{(-20x)}{3y^2}:\frac{(-4x^3}{5y}=\frac{-20x}{3y^2}.\frac{5y}{-4x^3}$
$=\frac{-20x}{-4x^3}.\frac{5y}{3y^2}$
$=\frac{5}{x^2}.\frac{5}{3y}=\frac{25}{3x^2y}$
7.
$\frac{(x+4)^2}{4x+12}:\frac{x+4}{3x+9}=\frac{(x+4)^2}{4(x+3)}.\frac{3(x+3)}{x+4}=\frac{(x+4)^2}{x+4}.\frac{3(x+3)}{4(x+3)}$
$=(x+4).\frac{3}{4}=\frac{3}{4}(x+4)$
10.
$\frac{x^2-4}{x^2-x}:\frac{x^2+2x}{x-1}=\frac{(x-2)(x+2)}{x(x-1)}.\frac{x-1}{x(x+2)}$
$=\frac{(x-2)(x+2)(x-1)}{x^2(x-1)(x+2)}=\frac{x-2}{x^2}$
11.
$\frac{4(x+3)}{3x^2-x}:\frac{x^2+3x}{1-3x}=\frac{4(x+3)}{x(3x-1)}.\frac{-(3x-1)}{x(x+3)}=\frac{-4(x+3)(3x-1)}{x(3x-1)x(x+3)}=\frac{-4}{x^2}$
12.
$\frac{4x+12}{(x+4)^2}:\frac{3(x+3)}{x+4}=\frac{4(x+3)}{(x+4)^2}.\frac{x+4}{3(x+3)}=\frac{4(x+3)(x+4)}{3(x+4)^2(x+3)}=\frac{4}{3(x+4)}$
13.
$(x^2-25):\frac{2x+10}{3x-7}=(x-5)(x+5).\frac{3x-7}{2(x+5)}=\frac{(3x-7)(x-5)}{2}$
14.
$\frac{5x-10}{x^2+7}:(2x-4)=\frac{5(x-2)}{(x^2+7).2(x-2)}=\frac{5}{2(x^2+7)}$
15.
$(4x^2-16):\frac{3x+6}{7x-2}=\frac{4(x^2-4)(7x-2)}{3x+6}=\frac{4(x-2)(x+2)(7x-2)}{3(x+2)}=\frac{4(x-2)(7x-2)}{3}$
16.
$\frac{x-y}{y-1}:\frac{x-y}{x-1}.\frac{x-1}{y-1}$
$=\frac{x-y}{y-1}.\frac{x-1}{x-y}.\frac{x-1}{y-1}$
$=\frac{x-1}{y-1}.\frac{x-1}{y-1}=\frac{(x-1)^2}{(y-1)^2}$
17.
$\frac{x+1}{x+2}.\frac{x+2}{x+3}:\frac{x+3}{x+1}$
$=\frac{x+1}{x+3}.\frac{x+1}{x+3}=\frac{(x+1)^2}{(x+3)^2}$
18.
$\frac{x+1}{x+2}:\frac{x+2}{x+3}.\frac{x+3}{x+1}$
$=\frac{x+1}{x+2}.\frac{x+3}{x+2}.\frac{x+3}{x+1}$
$=\frac{(x+1)(x+3)}{(x+2)^2}.\frac{x+3}{x+1}$
$=\frac{(x+3)^2}{(x+2)^2}$
19.
$\frac{x+1}{x+2}:\frac{x+2}{x+3}:\frac{x+3}{x+1}$
$=\frac{x+1}{x+2}.\frac{x+3}{x+2}.\frac{x+1}{x+3}$
$=\frac{(x+1)^2(x+3)}{(x+2)^2(x+3)}=\frac{(x+1)^2}{(x+2)^2}$
20.
$\frac{x^2+x}{x+2}:\frac{x+3}{x+2}.\frac{x+3}{x+1}$
$=\frac{x(x+1)}{x+2}.\frac{x+2}{x+3}.\frac{x+3}{x+1}$
$\frac{x(x+1)(x+2)(x+3)}{(x+2)(x+3)(x+1)}=x$
21.
$\frac{x+1}{x+2}(\frac{x+2}{x+3}:\frac{x+3}{x+1})$
$=\frac{x+1}{x+2}.(\frac{x+2}{x+3}.\frac{x+1}{x+3})$
$=\frac{x+1}{x+2}.\frac{(x+1)(x+2)}{(x+3)^2}=\frac{(x+1)^2}{(x+3)^2}$
22.
$\frac{x-2}{x+1}.\frac{x^2-2x-3}{x^2-5x+6}=\frac{(x-2)(x^2-2x-3)}{(x+1)(x^2-5x+6)}$
$=\frac{(x-2)(x+1)(x-3)}{(x+1)(x-2)(x-3)}=1$
23.
$\frac{x+1}{x^2-2x-8}.\frac{4-x}{x^2+x}=\frac{(x+1)(4-x)}{(x^2-2x-8)(x^2+x)}$
$=\frac{-(x+1)(x-4)}{(x+2)(x-4)x(x+1)}=\frac{-1}{x(x+2)}$
24.
$\frac{x^2+2}{4x+24}.\frac{x^2-36}{x^2+x-2}$
$=\frac{(x^2+2)(x^2-36}{(4x+24)(x^2+x-2)}$
$=\frac{(x^2+2)(x-6)(x+6)}{4(x+6)(x-1)(x+2)}=\frac{(x^2+2)(x-6)}{4(x-1)(x+2)}$
25.
$\frac{x^3-8}{5x+20}.\frac{x^2+4x}{x^2+2x+4}=\frac{(x^3-8)(x^2+4x)}{(5x+20)(x^2+2x+4)}$
$=\frac{(x-2)(x^2+2x+4)x(x+4)}{5(x+4)(x^2+2x+4)}$
$=\frac{(x-2)x}{5}$
26.
$\frac{(x-3)^3}{3x^2}:\frac{x^2-6x+9}{6x}=\frac{(x-3)^3}{3x^2}.\frac{6x}{x^2-6x+9}$
$=\frac{3x^2(x-3)^3}{6x(x-3)^2}=\frac{x(x-3)}{2}$
27.
$\frac{x^2+x}{5x^2-10x+5}:\frac{3x+3}{5x-5}=\frac{x(x+1)}{5(x-1)^2}.\frac{5(x-1)}{3(x+1)}$
$=\frac{x(x+1)5(x-1)}{5(x-1)^2.3(x+1)}$
$=\frac{x}{3(x-1)}$
28.
$\frac{6x-3}{5x^2+x}:\frac{1-8x^3}{25x^2+10x+1}$
$=\frac{3(2x-1)}{x(5x+1)}.\frac{(5x+1)^2}{(1-2x)(1+2x+4x^2)}$
$=\frac{3(2x-1)(5x+1)^2}{x(5x+1)(1-2x)(1+2x+4x^2)}$
$=\frac{-3(5x+1)}{x(4x^2+2x+1)}$
29.
$\frac{x^2+2x+1}{x^3-1}:\frac{x+1}{2x^2+2x+2}$
$=\frac{(x+1)^2}{(x-1)(x^2+x+1)}.\frac{2(x^2+x+1)}{x+1}$
$=\frac{2(x+1)^2(x^2+x+1)}{(x-1)(x^2+x+1)(x+1)}$
$=\frac{2(x+1)}{x-1}$
30.
$\frac{x+2}{x^2-5x+6}:\frac{x^2+3x+2}{x-2}$
$=\frac{x+2}{x^2-5x+6}.\frac{x-2}{x^2+3x+2}$
$=\frac{(x+2)(x-2)}{(x^2-5x+6)(x^2+3x+2)}$
$=\frac{(x+2)(x-2)}{(x-2)(x-3)(x+1)(x+2)}=\frac{1}{(x-3)(x+1)}$