Bài 1:
a: 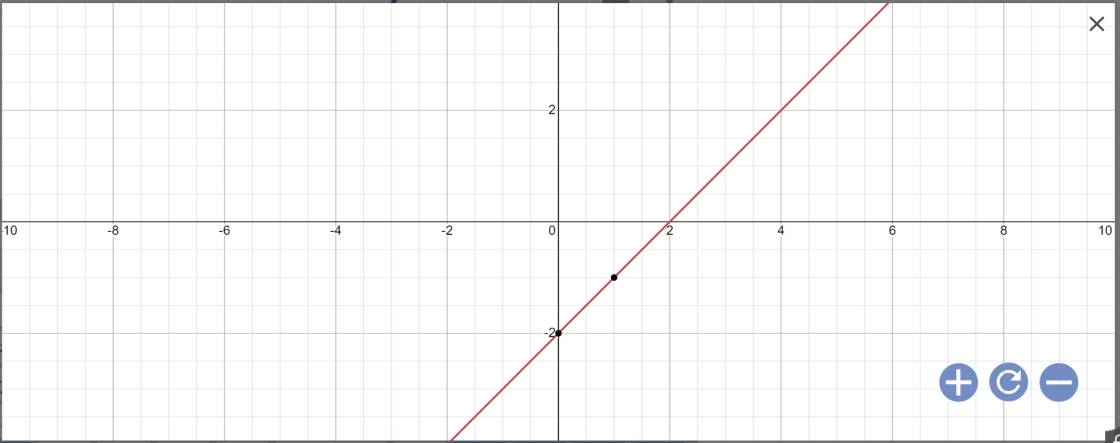
b: Thay x=2 và y=1 vào (2), ta được:
\(2\left(m+1\right)+3=1\)
=>2(m+1)=-2
=>m+1=-1
=>m=-1-1=-2
c: Để hai đường thẳng y=x-2 và y=(m+1)x+3 song song với nhau thì \(\left\{{}\begin{matrix}m+1=1\\3\ne-2\left(đúng\right)\end{matrix}\right.\)
=>m+1=1
=>m=0
Bài 3:
a: Xét ΔMAB có MD là phân giác
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)
=>\(\dfrac{AM}{4}=\dfrac{3}{2}\)
=>\(AM=4\cdot\dfrac{3}{2}=6\left(cm\right)\)
b: Xét ΔAMC có ME là phân giác
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\)
mà MC=MB
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MB}\)
=>\(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
=>\(AD\cdot EC=AE\cdot DB\)
Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
c: Xét ΔABM có DK//BM
nên \(\dfrac{DK}{BM}=\dfrac{AK}{AM}\left(1\right)\)
Xét ΔAMC có KE//MC
nên \(\dfrac{KE}{MC}=\dfrac{AK}{AM}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{DK}{BM}=\dfrac{KE}{MC}\)
mà BM=MC
nên DK=KE
=>K là trung điểm của DE