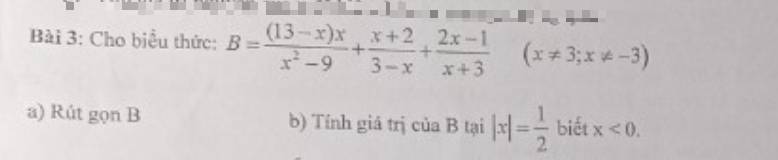a: \(B=\dfrac{x\left(13-x\right)}{x^2-9}+\dfrac{x+2}{3-x}+\dfrac{2x-1}{x+3}\)
\(=\dfrac{-x^2+13x}{\left(x-3\right)\left(x+3\right)}-\dfrac{x+2}{x-3}+\dfrac{2x-1}{x+3}\)
\(=\dfrac{-x^2+13x-\left(x+2\right)\left(x+3\right)+\left(2x-1\right)\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{-x^2+13x-x^2-5x-6+2x^2-7x+3}{\left(x-3\right)\cdot\left(x+3\right)}\)
\(=\dfrac{x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)
b: \(\left|x\right|=\dfrac{1}{2}\)
=>\(\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
mà x<0
nên \(x=-\dfrac{1}{2}\)(nhận)
Thay \(x=-\dfrac{1}{2}\) vào B, ta được:
\(B=\dfrac{1}{-\dfrac{1}{2}+3}=1:\dfrac{5}{2}=\dfrac{2}{5}\)