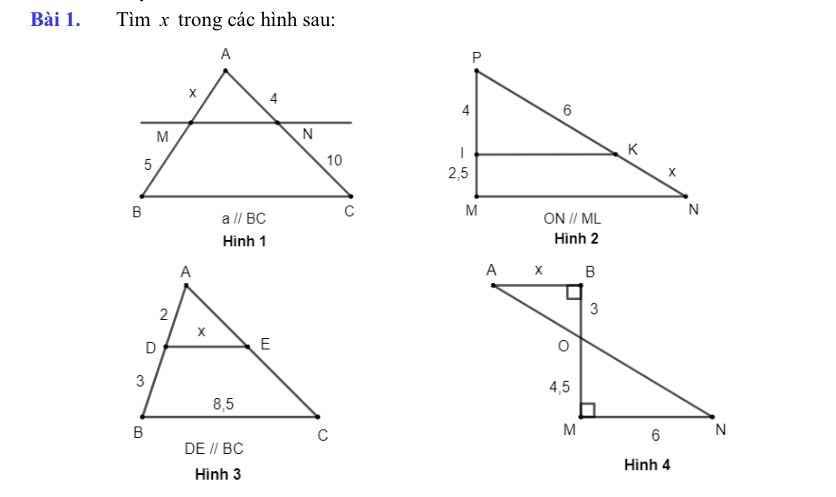
Hình 1:
Xét ΔABC có MN//BC
nên \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
=>\(\dfrac{x}{5}=\dfrac{4}{10}=\dfrac{2}{5}\)
=>x=2
Hình 2:
Xét ΔPMN có IK//MN
nên \(\dfrac{PI}{IM}=\dfrac{PK}{KN}\)
=>\(\dfrac{6}{x}=\dfrac{4}{2,5}\)
=>\(x=2.5\cdot\dfrac{6}{4}=3.75\)
Hình 3:
AB=AD+DB
=2+3
=5
Xét ΔABC có DE//BC
nên \(\dfrac{DE}{BC}=\dfrac{AD}{AB}\)
=>\(\dfrac{x}{8,5}=\dfrac{2}{5}\)
=>\(x=8,5\cdot\dfrac{2}{5}=3,4\)
Hình 4:
Xét ΔOMN vuông tại M và ΔOBA vuông tại B có
\(\widehat{MON}=\widehat{BOA}\)(hai góc đối đỉnh)
Do đó; ΔOMN~ΔOBA
=>\(\dfrac{OM}{OB}=\dfrac{ON}{OA}=\dfrac{MN}{AB}\)
=>\(\dfrac{6}{AB}=\dfrac{4.5}{3}=\dfrac{3}{2}\)
=>AB=4
Đúng 1
Bình luận (1)
