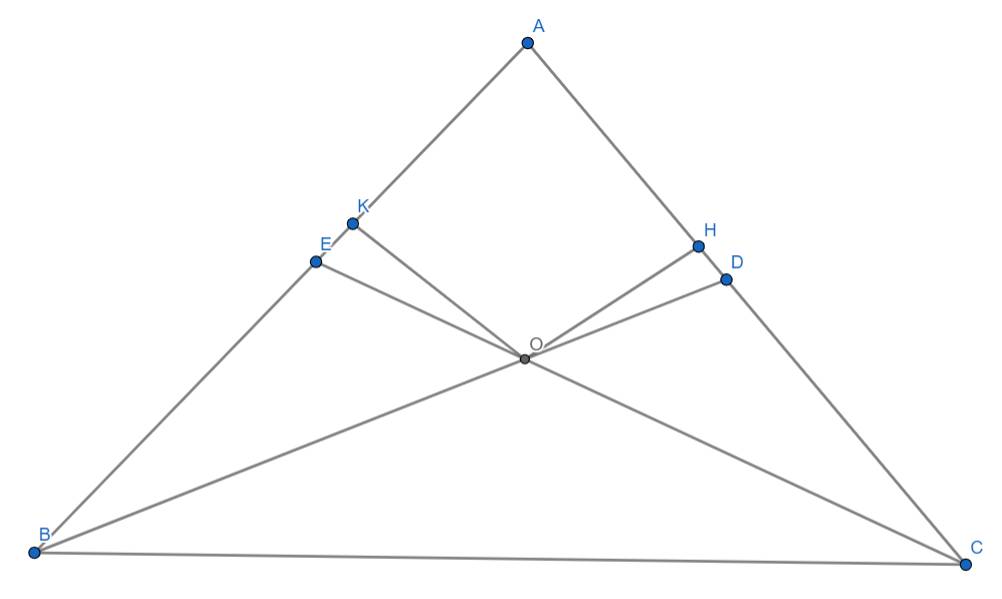
a) Ta có: \(\widehat{ABC}=\widehat{ACB}\) (vì tam giác ABC cần tại A)
\(\Rightarrow\widehat{DBC}=\widehat{ECB}\) (vì BD và CE là phân giác của hai góc trên)
Xét ΔBCD và ΔCBE có:
\(\widehat{ABC}=\widehat{ACB}\)
\(\widehat{DBC}=\widehat{ECB}\) (cmt)
\(BC\) là cạnh chung
\(\Rightarrow\Delta BCD=\Delta CBE\left(g.c.g\right)\)
b) Ta có: \(\widehat{ABC}=\widehat{ACB}\Rightarrow\widehat{ABO}=\widehat{ACO}\) (vì BD và CE là phân giác của hai góc trên)
\(\Delta BCD=\Delta CBE\left(cmt\right)\Rightarrow CD=BE\) (hai cạnh tương ứng)
Xét ΔBOE và ΔCOD có:
\(\widehat{ABO}=\widehat{ACO}\) (cmt)
\(CD=BE\left(cmt\right)\)
\(\widehat{EOB}=\widehat{DOC}\) (đối đỉnh)
\(\Rightarrow\Delta BOE=\Delta COD\left(g.c.g\right)\)
\(\Rightarrow OC=OB\) (hai cạnh tương ứng)
c) Ta có: \(\Delta BOE=\Delta COD\left(cmt\right)\Rightarrow\left\{{}\begin{matrix}\widehat{BEO}=\widehat{CDO}\\OE=OD\end{matrix}\right.\)
\(\widehat{BEO}=\widehat{CDO}\) (hai góc tương ứng)
\(\Rightarrow180^o-\widehat{KEO}=180^o-\widehat{HDO}\)
\(\Rightarrow\widehat{KEO}=\widehat{HDO}\)
Xét hai tam giác vuông KOE và HOD có:
\(OE=OD\left(cmt\right)\)
\(\widehat{KEO}=\widehat{HDO}\left(cmt\right)\)
\(\Rightarrow\Delta KOE=\Delta HOD\) (cạnh huyền - góc nhọn)
\(\Rightarrow OK=OH\) (hai cạnh tương ứng)
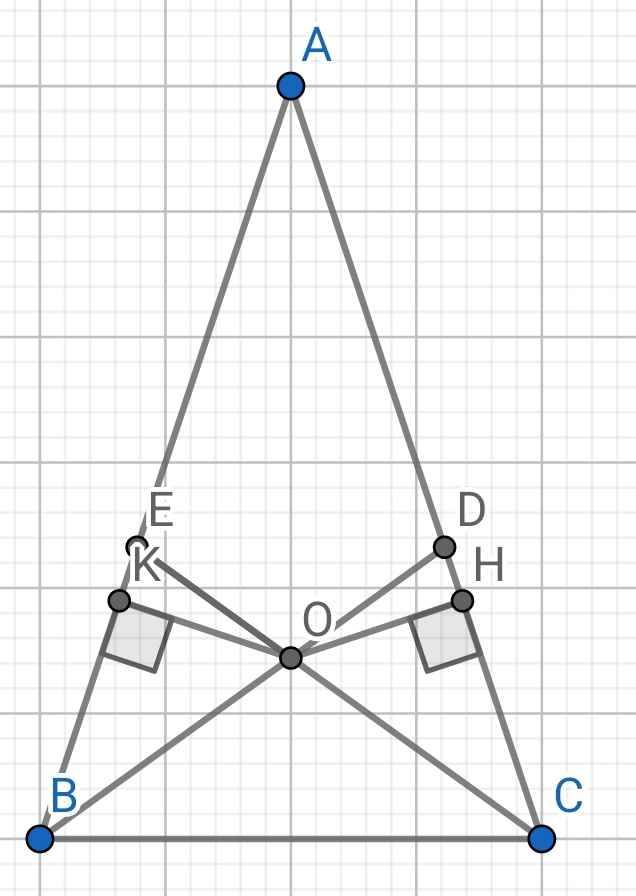
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB
⇒ ∠EBC = ∠DCB
Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD = ABC : 2
Do CE là tia phân giác của ∠ACB (gt)
⇒ ∠ACE = ∠BCE = ∠ACB : 2
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABD = ∠CBD = ∠ACE = ∠BCE
Xét ∆BCD và ∆CBE có:
∠CBD = ∠BCE (cmt)
BC là cạnh chung
∠DCB = ∠EBC (cmt)
⇒ ∆BCD = ∆CBE (g-c-g)
b) Do ∠BCE = ∠CBD (cmt)
⇒ ∠BCO = ∠CBO
⇒ ∆OBC cân tại O
⇒ OB = OC
c) Do ∠ABD = ∠ACE (cmt)
⇒ ∠KBO = ∠HCO
Xét hai tam giác vuông: ∆KBO và ∆HCO có:
OB = OC (cmt)
∠KBO = ∠HCO (cmt)
∆KBO = ∆HCO (cạnh huyền - góc nhọn)
⇒ OK = OH (hai cạnh tương ứng)
















