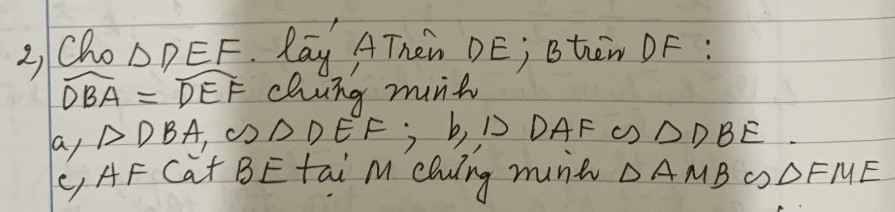a: Xét ΔDBA và ΔDEF có
\(\widehat{DBA}=\widehat{DEF}\)
\(\widehat{D}\) chung
Do đó: ΔDBA~ΔDEF
b: Ta có: ΔDBA~ΔDEF
=>\(\dfrac{DB}{DE}=\dfrac{DA}{DF}\)
=>\(\dfrac{DB}{DA}=\dfrac{DE}{DF}\)
Xét ΔDBE và ΔDAF có
\(\dfrac{DB}{DA}=\dfrac{DE}{DF}\)
\(\widehat{BDE}\) chung
Do đó: ΔDBE~ΔDAF
c: Ta có: ΔDBE~ΔDAF
=>\(\widehat{DEB}=\widehat{DFA}\)
Xét ΔMAE và ΔMBF có
\(\widehat{MEA}=\widehat{MFB}\)
\(\widehat{AME}=\widehat{BMF}\)(hai góc đối đỉnh)
Do đó: ΔMAE~ΔMBF
=>\(\dfrac{MA}{MB}=\dfrac{ME}{MF}\)
=>\(\dfrac{MA}{ME}=\dfrac{MB}{MF}\)
Xét ΔMAB và ΔMEF có
\(\dfrac{MA}{ME}=\dfrac{MB}{MF}\)
\(\widehat{AMB}=\widehat{EMF}\)
Do đó: ΔMAB~ΔMEF