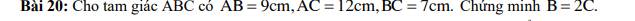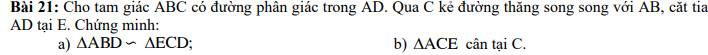Bài 20:
Xét ΔABC có \(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(=\dfrac{9^2+7^2-12^2}{2\cdot9\cdot7}=\dfrac{-1}{9}\)
Xét ΔABC có \(cosC=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
\(=\dfrac{12^2+7^2-9^2}{2\cdot12\cdot7}=\dfrac{2}{3}\)
\(cos\left(2C\right)=2\cdot cos^2C-1=2\cdot\left(\dfrac{2}{3}\right)^2-1=-\dfrac{1}{9}\)
=>\(cos\left(2C\right)=cosB\)
=>\(\widehat{B}=2\cdot\widehat{C}\)
Bài 21:
a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)(hai góc đối đỉnh)
\(\widehat{ABD}=\widehat{ECD}\)(hai góc so le trong, AB//CE)
Do đó: ΔABD~ΔECD
b: Ta có: \(\widehat{CEA}=\widehat{BAD}\)(hai góc so le trong, AB//CE)
\(\widehat{BAD}=\widehat{CAE}\)(AD là phân giác của góc BAC)
Do đó: \(\widehat{CEA}=\widehat{CAE}\)
=>ΔCAE cân tại C