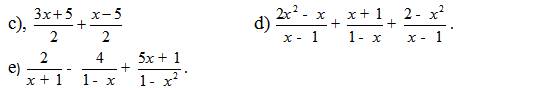c/
\(\frac{3x+5}{2}+\frac{x-5}{2}=\frac{3x+5+x-5}{2}=\frac{4x}{2}=2x\)
d/ ĐKXĐ: $x\neq 1$
\(=\frac{2x^2-x}{x-1}-\frac{x+1}{x-1}+\frac{2-x^2}{x-1}\\ =\frac{2x^2-x-x-1+2-x^2}{x-1}\\ =\frac{x^2-2x+1}{x-1}=\frac{(x-1)^2}{x-1}=x-1\)
e/ ĐKXĐ: $x\neq \pm 1$
\(=\frac{2(x-1)}{(x+1)(x-1)}+\frac{4(x+1)}{(x-1)(x+1)}-\frac{5x+1}{(x-1)(x+1)}\\ =\frac{2x-2+4x+4-5x-1}{(x-1)(x+1)}\\ =\frac{x+1}{(x-1)(x+1)}=\frac{1}{x-1}\)
Đúng 1
Bình luận (0)
