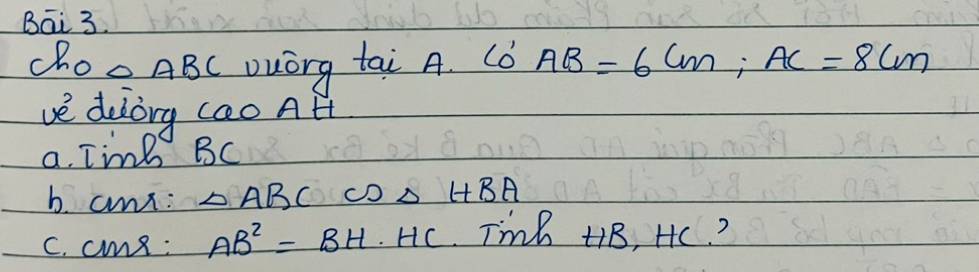a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{6^2+8^2}=\sqrt{100}=10\left(cm\right)\)
b) Xét ΔABC và ΔHBA có:
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right)\)
\(\widehat{BCA}=\widehat{BAH}\) (cùng phụ với \(\widehat{B}\))
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
c) Sửa chứng minh: \(AB^2=BC\cdot HB\)
Ta có: \(\Delta ABC\sim\Delta HBA\)
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Rightarrow AB^2=BC\cdot HB\)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Mà: \(BC=HB+HC\Rightarrow HC=BC-HB=10-3,6=6,4\left(cm\right)\)