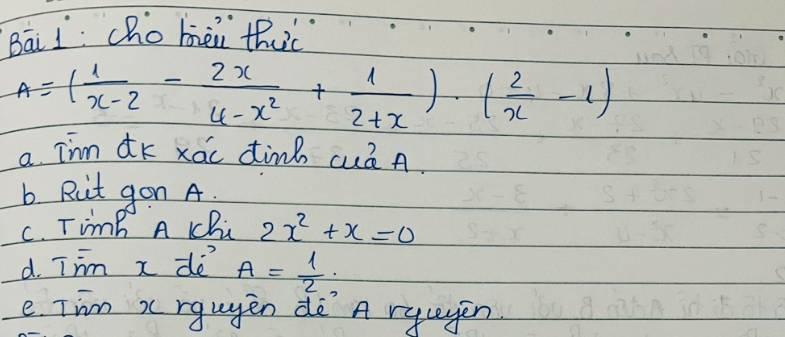a) ĐKXĐ:
\(\left\{{}\begin{matrix}x-2\ne0\\4-x^2\ne0\\2+x\ne0\\x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-2\\x\ne0\end{matrix}\right.\)
b) \(A=\left(\dfrac{1}{x-2}-\dfrac{2x}{4-x^2}+\dfrac{1}{2+x}\right).\left(\dfrac{2}{x}-1\right)\)
\(=\left(\dfrac{1}{x-2}+\dfrac{2x}{x^2-4}+\dfrac{1}{x+2}\right).\left(\dfrac{2-x}{x}\right)\)
\(=\dfrac{x+2+2x+x-2}{\left(x-2\right)\left(x+2\right)}.\dfrac{2-x}{x}\)
\(=\dfrac{4x}{\left(x-2\right)\left(x+2\right)}.\dfrac{-\left(x-2\right)}{x}\)
\(=\dfrac{-4}{x+2}\)
c) \(2x^2+x=0\)
\(\Leftrightarrow x\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=-\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\)
Với \(x=-\dfrac{1}{2}\Rightarrow A=\dfrac{-4}{-\dfrac{1}{2}+2}=-\dfrac{8}{3}\)
Vậy khi \(2x^2+x=0\) thì \(A=-\dfrac{8}{3}\)
d) \(A=\dfrac{1}{2}\Leftrightarrow\dfrac{-4}{x+2}=\dfrac{1}{2}\)
\(\Leftrightarrow x+2=-8\)
\(\Leftrightarrow x=-8-2\)
\(\Leftrightarrow x=-10\) (nhận)
Vậy \(A=\dfrac{1}{2}\) khi \(x=-10\)
e) \(A\) nguyên khi \(-4⋮\left(x+2\right)\)
\(\Rightarrow x+2\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x\in\left\{-6;-4;-3;-1;0;2\right\}\)
Mà \(x\ne0;x\ne2\)
\(\Rightarrow x\in\left\{-6;-4;-3;-1\right\}\)
Vậy khi \(x\in\left\{-6;-4;-3;-1\right\}\) thì \(A\) nguyên