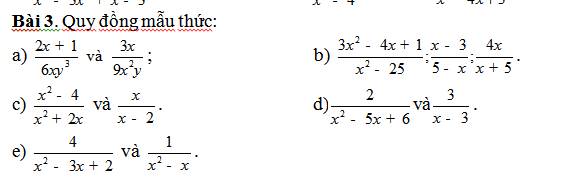a: \(MTC=18x^2y^3\)
\(\dfrac{2x+1}{6xy^3}=\dfrac{\left(2x+1\right)\cdot3x}{18x^2y^3}=\dfrac{6x^2+3x}{18x^2y^3}\)
\(\dfrac{3x}{9x^2y}=\dfrac{3x\cdot2\cdot y^2}{18x^2y^3}=\dfrac{6xy^2}{18x^2y^3}\)
b: \(MTC=\left(x-5\right)\left(x+5\right)\)
\(\dfrac{3x^2-4x+1}{x^2-25}=\dfrac{3x^2-4x+1}{\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{x-3}{5-x}=\dfrac{3-x}{x-5}=\dfrac{\left(3-x\right)\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{3x+15-x^2-5x}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-x^2-2x+15}{\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{4x}{x+5}=\dfrac{4x\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}=\dfrac{4x^2-20x}{\left(x+5\right)\left(x-5\right)}\)
c: MTC=x(x+2)(x-2)
\(\dfrac{x^2-4}{x^2+2x}=\dfrac{x^2-4}{x\left(x+2\right)}=\dfrac{\left(x^2-4\right)\left(x-2\right)}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x^3-2x^2-4x+8}{x\left(x+2\right)\left(x-2\right)}\)
\(\dfrac{x}{x-2}=\dfrac{x\cdot x\left(x+2\right)}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^3+2x^2}{x\left(x-2\right)\left(x+2\right)}\)
d: MTC=(x-3)(x-2)
\(\dfrac{2}{x^2-5x+6}=\dfrac{2}{\left(x-3\right)\left(x-2\right)}\)
\(\dfrac{3}{x-3}=\dfrac{3\left(x-2\right)}{\left(x-3\right)\left(x-2\right)}=\dfrac{3x-6}{\left(x-3\right)\left(x-2\right)}\)
e: \(MTC=x\left(x-1\right)\left(x-2\right)\)
\(\dfrac{4}{x^2-3x+2}=\dfrac{4}{\left(x-1\right)\left(x-2\right)}=\dfrac{4x}{x\left(x-1\right)\left(x-2\right)}\)
\(\dfrac{1}{x^2-x}=\dfrac{1}{x\left(x-1\right)}=\dfrac{x-2}{x\left(x-1\right)\left(x-2\right)}\)