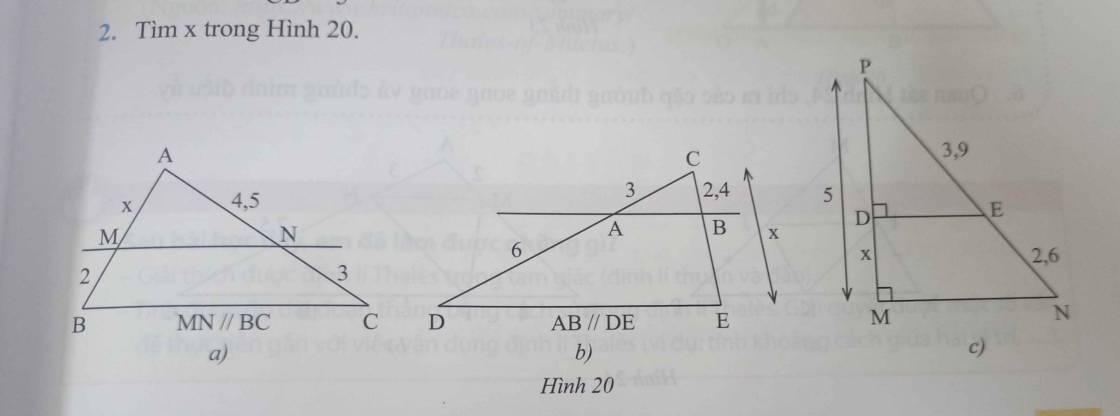
a: Xét ΔABC có MN//BC
nên \(\dfrac{AM}{MB}=\dfrac{AN}{NC}\)
=>\(\dfrac{x}{2}=\dfrac{4.5}{3}=\dfrac{3}{2}\)
=>x=3
b:
CA+AD=CD
=>CD=3+6
=>CD=9
Xét ΔCDE có AB//DE
nên \(\dfrac{CB}{CE}=\dfrac{CA}{CD}\)
=>\(\dfrac{2.4}{x}=\dfrac{3}{9}=\dfrac{1}{3}\)
=>\(x=2.4\cdot3=7,2\)
c:
PE+EN=PN
=>PN=3,9+2,6=6,5
DE\(\perp\)PM
MN\(\perp\)PM
Do đó: DE//MN
Xét ΔPMN có DE//MN
nên \(\dfrac{PD}{PM}=\dfrac{PE}{PN}\)
=>\(\dfrac{PD}{5}=\dfrac{3.9}{6.5}=\dfrac{3}{5}\)
=>\(PD=\dfrac{3}{5}\cdot5=3\)
Ta có: PD+DM=PM
=>x+3=5
=>x=2
Đúng 1
Bình luận (0)
