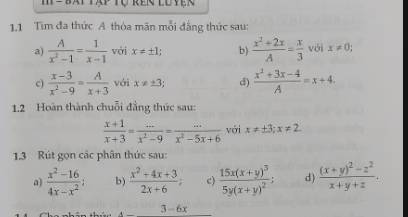1.3:
a: ĐKXĐ: \(x\notin\left\{0;4\right\}\)
\(\dfrac{x^2-16}{4x-x^2}\)
\(=-\dfrac{\left(x-4\right)\left(x+4\right)}{x\left(x-4\right)}\)
\(=-\dfrac{x+4}{x}\)
b: ĐKXĐ: x<>-3
\(\dfrac{x^2+4x+3}{2x+6}\)
\(=\dfrac{\left(x+1\right)\left(x+3\right)}{2\left(x+3\right)}\)
\(=\dfrac{x+1}{2}\)
c: ĐKXĐ: y<>0 và x<>-y
\(\dfrac{15x\left(x+y\right)^3}{5y\left(x+y\right)^2}\)
\(=\dfrac{5\cdot x\cdot3\cdot\left(x+y\right)^2\cdot\left(x+y\right)}{5y\left(x+y\right)^2}\)
\(=\dfrac{3x\left(x+y\right)}{y}\)
d: ĐKXĐ: x+y+z<>0
\(\dfrac{\left(x+y\right)^2-z^2}{x+y+z}\)
\(=\dfrac{\left(x+y+z\right)\left(x+y-z\right)}{x+y+z}\)
=x+y-z
Bài 1.2:
Đặt \(\dfrac{x+1}{x+3}=\dfrac{A}{x^2-9}=\dfrac{B}{x^2-5x+6}\)
=>\(\left\{{}\begin{matrix}A=\dfrac{\left(x^2-9\right)\cdot\left(x+1\right)}{x+3}=\dfrac{\left(x+3\right)\left(x-3\right)\left(x+1\right)}{x+3}\\B=\dfrac{\left(x^2-5x+6\right)\left(x+1\right)}{x+3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}A=\left(x-3\right)\left(x+1\right)=x^2-2x-3\\B=\dfrac{x^3-4x^2+x+6}{x+3}\end{matrix}\right.\)