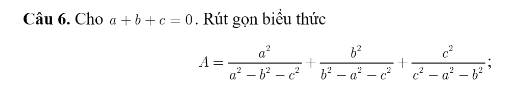a+b+c=0
=>\(\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
\(A=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-a^2-c^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{\left(a-b\right)\left(a+b\right)-c^2}+\dfrac{b^2}{\left(b-a\right)\left(b+a\right)-c^2}+\dfrac{c^2}{\left(c-a\right)\left(c+a\right)-b^2}\)
\(=\dfrac{a^2}{-c\cdot\left(a-b\right)-c^2}+\dfrac{b^2}{\left(b-a\right)\cdot\left(-c\right)-c^2}+\dfrac{c^2}{-b\left(c-a\right)-b^2}\)
\(=\dfrac{a^2}{-c\left(a-b+c\right)}+\dfrac{b^2}{c\left(-b+a-c\right)}+\dfrac{c^2}{b\left(-c+a-b\right)}\)
\(=\dfrac{a^2}{-c\cdot\left(-b-b\right)}+\dfrac{b^2}{c\cdot\left(a+a\right)}+\dfrac{c^2}{b\left(a+a\right)}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
\(=\dfrac{\left(a+b\right)^3-3ab\left(a+b\right)+c^3}{2abc}\)
\(=\dfrac{\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\cdot\left(-c\right)}{2bac}\)
\(=\dfrac{3bac}{2bca}=\dfrac{3}{2}\)