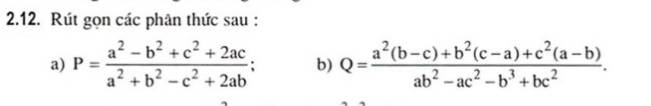\(P=\dfrac{a^2+2ac+c^2-b^2}{a^2+2ab+b^2-c^2}=\dfrac{\left(a+c\right)^2-b^2}{\left(a+b\right)^2-c^2}\)
\(=\dfrac{\left(a+c+b\right)\left(a+c-b\right)}{\left(a+b+c\right)\left(a+b-c\right)}=\dfrac{a-b+c}{a+b-c}\)
\(Q=\dfrac{a^2b-a^2c+b^2c-ab^2+c^2\left(a-b\right)}{ab^2-b^3-ac^2+bc^2}=\dfrac{ab\left(a-b\right)-c\left(a^2-b^2\right)+c^2\left(a-b\right)}{b^2\left(a-b\right)-c^2\left(a-b\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)}{\left(b^2-c^2\right)\left(a-b\right)}=\dfrac{\left(a-b\right)\left(ab-ac-bc+c^2\right)}{\left(b-c\right)\left(b+c\right)\left(a-b\right)}\)
\(=\dfrac{\left(a-b\right)\left[a\left(b-c\right)-c\left(b-c\right)\right]}{\left(b-c\right)\left(b+c\right)\left(a-b\right)}=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(b-c\right)\left(b+c\right)\left(a-b\right)}\)
\(=\dfrac{a-c}{b+c}\)