B. Tự luận
Bài 1:
a)
\(\left(x-2\right)\left(x+2\right)-x^2=x^2-4-x^2=-4\)
b)
\(\left(x+1\right)\left(x^2-x+1\right)+5-x^3=x^3-1+5-x^3=4\)
Bài 2
a)
\(x^2-4xy+4y^2=x^2-2.x.2y+\left(2y\right)^2=\left(x-2y\right)^2\)
b)
\(3x^2-3xy+5x-5y=3x\left(x-y\right)+5\left(x-y\right)=\left(x-y\right)\left(3x+5\right)\)
c)
\(x^4-9x^3+16x^2+18x+4\\ =x^4-4x^3-2x^2-5x^3+20x^2+10x-2x^2+8x+4\\ =x^2\left(x^2-4x-2\right)-5x\left(x^2-4x-2\right)-2\left(x^2-4x-2\right)\\ =\left(x^2-4x-2\right)\left(x^2-5x-2\right)\)
I: Trắc nghiệm
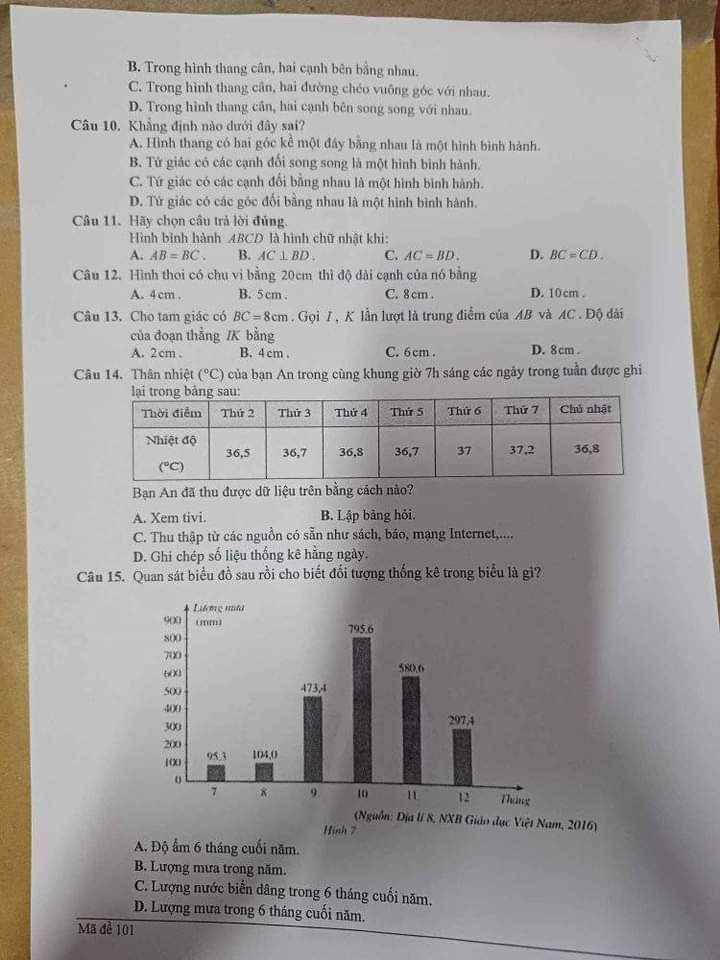
Câu 10: A
Câu 11: C
Câu 12: B
Câu 13: B
Câu 14: D
Câu 15: D
II: Tự luận
Bài 3:
a: Xét ΔABC có
D,E lần lượt là trung điểm của CB,CA
=>DE là đường trung bình của ΔABC
=>DE//AB và \(DE=\dfrac{1}{2}AB=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
b: Xét ΔDAB có DM là phân giác
nên \(\dfrac{AM}{MB}=\dfrac{AD}{DB}\)
=>\(AM\cdot DB=AD\cdot BM\)
Xét ΔDAC có DN là phân giác
nên \(\dfrac{AN}{NC}=\dfrac{AD}{DC}\)
=>\(\dfrac{AN}{NC}=\dfrac{AD}{DB}\)(Do DB=DC)
=>\(\dfrac{AN}{NC}=\dfrac{AM}{MB}\)
Xét ΔABC có \(\dfrac{AN}{NC}=\dfrac{AM}{MB}\)
nên MN//BC