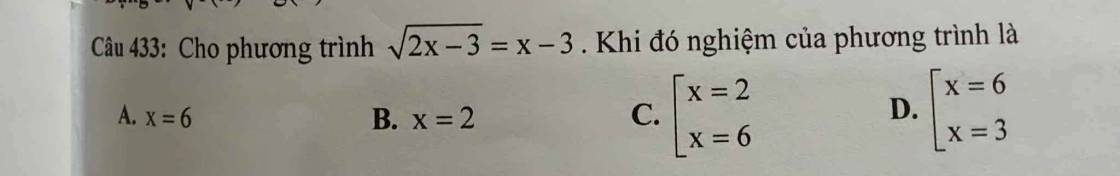\(\sqrt{2x-3}=x-3\left(dkxd:x\ge\dfrac{3}{2}\right)\)
\(\Leftrightarrow\left|2x-3\right|=x^2-6x+9\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x^2-6x+9\\3-2x=x^2-6x+9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-x^2+8x-12=0\\-x^2+4x-6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=2\end{matrix}\right.\) \(\left(tmdk\right)\)
Chọn C.
Vì:
\(\sqrt{2x-3}=x-3\)
⇔\(\sqrt{2x-3}^2=\left(x-3\right)^2\)
⇔\(2x-3=x^2+2x\left(-3\right)+\left(-3\right)^2\)
⇔\(2x-3=x^2-2\cdot3x+9\)
⇔\(2x-3=x^2-6x+9\)
⇔\(2x-3-x^2+6x-9=x^2-6x+9-x^2+6x-9\)
⇔\(8x-x^2-12=0\)
⇔\(x^2-8x+12=0\)
⇔\(x^2-6x-2x+12=0\)
⇔\(x\left(\dfrac{x^2}{x}-\dfrac{2\cdot3x}{x}\right)+2\left(-\dfrac{2x}{2}+\dfrac{2^2\cdot3}{2}\right)=0\)
⇔\(x\left[x^{2-1}-\left(2\cdot3\right)\right]+2\left[-x+2^{2-1}\cdot3\right]=0\)
⇔\(x\left(x-6\right)+2\left(-x+2\cdot3\right)=0\)
⇔\(x\left(x-6\right)+2\left(-x+6\right)=0\)
⇔\(\left(x-6\right)\left(\dfrac{x\left(x-6\right)}{x-6}+\dfrac{2\left(-x+6\right)}{x-6}\right)=0\)
⇔\(\left(x-6\right)\left(x-2\right)=0\)
\(\left\{{}\begin{matrix}x-6=0\\x-2=0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x=0+6=6\\x=0+2=2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x=6\\x=2\end{matrix}\right.\)
⇒ Chọn C