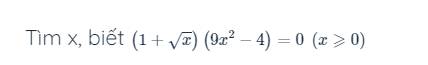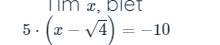\(\left(1+\sqrt{x}\right)\left(9x^2-4\right)=0\)
=>\(9x^2-4=0\left(1+\sqrt{x}>=1>0\forall x>=0\right)\)
\(\Leftrightarrow9x^2=4\)
=>\(x^2=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}x=\dfrac{2}{3}\left(nhận\right)\\x=-\dfrac{2}{3}\left(loại\right)\end{matrix}\right.\)
\(5\left(x-\sqrt{4}\right)=-10\)
=>\(5\left(x-2\right)=-10\)
=>x-2=-2
=>x=0
\(\left(1+\sqrt{x}\right)\left(9x^2-4\right)=0\left(ĐKx\ge0\right)\\ \Rightarrow\left[{}\begin{matrix}1+\sqrt{x}=0\\9x^2-4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\sqrt{x}=-1\left(ktm\right)\\9x^2=4\left(1\right)\end{matrix}\right.\\ \left(1\right)\Rightarrow x^2=\dfrac{4}{4}\\ \Rightarrow x=\sqrt{\dfrac{4}{9}}\\ \Rightarrow x=\pm\dfrac{2}{3}\\ \Rightarrow x=\dfrac{2}{3}\left(tm\right)\\ 5\cdot\left(x-\sqrt{4}\right)=-10\\ \Rightarrow x-2=-10:5\\ \Rightarrow x-2=-2\\ \Rightarrow x=-2+2\\ \Rightarrow x=0\)