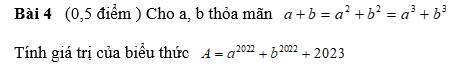Lời giải:
$a+b=a^2+b^2=a^3+b^3$
$\Rightarrow (a^3+b^3)(a+b)=(a^2+b^2)^2$
$\Leftrightarrow a^3b+ab^3=2a^2b^2$
$\Leftrightarrow ab(a^2+b^2-2ab)=0$
$\Leftrightarrow ab(a-b)^2=0$
$\Leftrightarrow a=0$ hoặc $b=0$ hoặc $a=b$
TH1: $a=0$ thì:
Từ $a+b=a^2+b^2\Rightarrow b=b^2\Rightarrow b(b-1)=0$
$\Rightarrow b=0$ hoặc $b=1$ (tm)
Khi đó: $A=0^{2022}+0^{2022}+2023=2023$ hoặc $A=0^{2022}+1^{2022}+2023=2024$
TH2: $b=0$ thì tương tự TH1 ta cũng có $A=2023$ hoặc $A=2024$
TH3: $a=b$ thì:
$a+b=a^2+b^2$
$\Leftrightarrow 2a=2a^2\Leftrightarrow a=a^2\Leftrightarrow a=0$ hoặc $a=1$
$\Rightarrow b=0$ hoặc $b=1$ (tm)
Khi đó: $A=1^{2022}+1^{2022}+2023=2025$ hoặc $A=0^{2022}+0^{2022}+2023=2023$
Vậy $A\in \left\{2023; 2024; 2025\right\}$