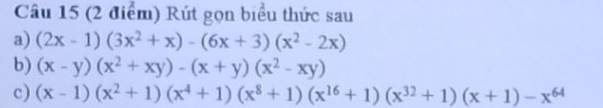a: \(\left(2x-1\right)\left(3x^2+x\right)-\left(6x+3\right)\left(x^2-2x\right)\)
\(=6x^3+2x^2-3x^2-x-6x^3+12x^2-3x^2+6x\)
\(=8x^2+5x\)
b: \(\left(x-y\right)\left(x^2+xy\right)-\left(x+y\right)\left(x^2-xy\right)\)
\(=x^3+x^2y-x^2y-xy^2-x^3+x^2y-x^2y+xy^2\)
=0
c: \(\left(x-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)\left(x+1\right)-x^{64}\)
\(=\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(=\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(=\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(=\left(x^{16}-1\right)\left(x^{16}+1\right)\left(x^{32}+1\right)-x^{64}\)
\(=\left(x^{32}-1\right)\left(x^{32}+1\right)-x^{64}\)
\(=x^{64}-1-x^{64}=-1\)