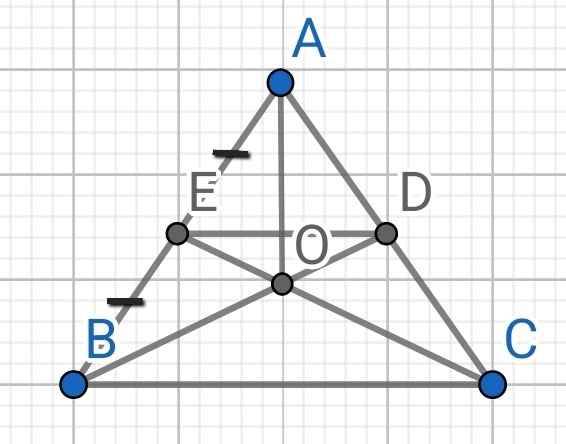
 a) Ta có:
a) Ta có:
∠ABC = ∠AED = 50⁰ (gt)
Mà ∠ABC và ∠AED là hai góc đồng vị
⇒ DE // BC
b) Do ∆ABC cân tại A
⇒ ∠ABC = ∠ACB = 50⁰
⇒ ∠EBC = ∠DCB = 50⁰
Tứ giác BCDE có:
DE // BC (cmt)
⇒ BCDE là hình thang
Mà ∠EBC = ∠DCB (cmt)
⇒ BCDE là hình thang cân
c) Do E là trung điểm của AB (gt)
⇒ CE là đường trung tuyến của ∆ABC
∆ABC có:
DE // BC (cmt)
E là trung điểm của AB
⇒ D là trung điểm của AC
⇒ BD là đường trung tuyến của ∆ABC
Mà O là giao điểm của BD và CE
⇒ AO là đường trung tuyến thứ ba của ∆ABC
Lại có:
∆ABC cân tại A (gt)
⇒ AO cũng là đường phân giác của ∆ABC
⇒ AO là phân giác của ∠BAC
















