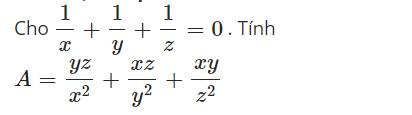Question

Answer 1

Lời giải:

$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$

$\Rightarrow \frac{xy+yz+xz}{xyz}=0\Rightarrow xy+yz+xz=0$

Đặt $xy=a; yz=b; zx=c\Rightarrow a+b+c=0$

Khi đó:

$A=\frac{(xy)^3+(yz)^3+(xz)^3}{x^2y^2z^2}=\frac{a^3+b^3+c^3}{abc}$

$=\frac{(a+b)^3-3ab(a+b)+c^3}{abc}$

$=\frac{(-c)^3-3ab(-c)+c^3}{abc}=\frac{-c^3+3abc+c^3}{abc}=\frac{3abc}{abc}=3$

Answer 2

Lời giải:

$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0$

$\Rightarrow \frac{xy+yz+xz}{xyz}=0\Rightarrow xy+yz+xz=0$

Đặt $xy=a; yz=b; zx=c\Rightarrow a+b+c=0$

Khi đó:

$A=\frac{(xy)^3+(yz)^3+(xz)^3}{x^2y^2z^2}=\frac{a^3+b^3+c^3}{abc}$

$=\frac{(a+b)^3-3ab(a+b)+c^3}{abc}$

$=\frac{(-c)^3-3ab(-c)+c^3}{abc}=\frac{-c^3+3abc+c^3}{abc}=\frac{3abc}{abc}=3$