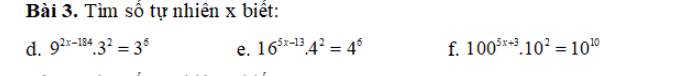`d)9^(2x-184).3^2=3^6`
`=>9^(2x-184)=3^6:3^2`
`=>9^(2^x-184)=3^4`
`=>9^(2x-184)=(3^2)^2`
`=>9^(2x-184)=9^2`
`=>2x-184=2`
`=>2x=186`
`=>x=93`
Vậy `x=93`
__
`e)16^(5x-13).4^2=4^6`
`=>16^(5x-13)=4^6:4^2`
`=>16^(5x-13)=4^4`
`=>16^(5x-13)=16^2`
`=>5x-13=2`
`=>5x=15`
`=>x=3`
Vậy `x=3`
__
`f)100^(5x+3).10^2=10^10`
`=>100^(5x+3)=10^8`
`=>100^(5x+3)=(10^2)^4`
`=>100^(5x+3)=100^4`
`=>5x+3=4`
`=>5x=1`
`=>x=1/5`
Vậy `x=1/5`
d) \(9^{2x-184}.3^2=3^6\)
\(9^{2x-184}=3^4=9^2\)
\(2x-184=2\)
\(x=93\)(TM)
e) \(16^{5x-13}.4^2=4^6\)
\(16^{5x-13}=4^4=16^2\)
\(5x-13=2\)
\(x=3\)(TM)
f) \(100^{5x+3}.10^2=10^{10}\)
\(100^{5x+3}=10^8=100^4\)
\(5x+3=4\)
\(x=\dfrac{1}{5}\)(Loại)
d) \(9^{2x-184}\cdot3^2=3^6\)
\(\Rightarrow\left(3^2\right)^{2x-184}=3^6:3^2\)
\(\Rightarrow3^{4x-368}=3^4\)
\(\Rightarrow4x-368=4\)
\(\Rightarrow4x=4+368\)
\(\Rightarrow4x=372\)
\(\Rightarrow x=372:4=93\left(tm\right)\)
\(---\)
e) \(16^{5x-13}\cdot4^2=4^6\)
\(\Rightarrow\left(4^2\right)^{5x-13}=4^6:4^2\)
\(\Rightarrow4^{10x-26}=4^4\)
\(\Rightarrow10x-26=4\)
\(\Rightarrow10x=4+26\)
\(\Rightarrow10x=30\)
\(\Rightarrow x=30:10=3\left(tm\right)\)
\(---\)
f) \(100^{5x+3}\cdot10^2=10^{10}\)
\(\Rightarrow\left(10^2\right)^{5x+3}=10^{10}:10^2\)
\(\Rightarrow10^{10x+6}=10^8\)
\(\Rightarrow10x+6=8\)
\(\Rightarrow10x=8-6\)
\(\Rightarrow10x=2\)
\(\Rightarrow x=2:10=\dfrac{1}{5}\left(ktm\right)\)
\(Toru\)