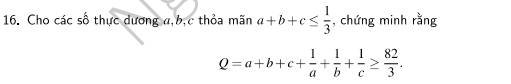Question

Answer 1

Lời giải:

Áp dụng BĐT Bunhiacopxky:

$(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})(a+b+c)\geq (1+1+1)^2$
$\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq \frac{9}{a+b+c}$

$\Rightarrow Q\geq a+b+c+\frac{9}{a+b+c}$

Áp dụng BĐT Cô-si:

$a+b+c+\frac{1}{9(a+b+c)}\geq 2\sqrt{\frac{1}{9}}=\frac{2}{3}$

$\frac{80}{9(a+b+c)}\geq \frac{80}{9.\frac{1}{3}}=\frac{80}{3}$ do $a+b+c\leq \frac{1}{3}$

$\Rightarrow Q\geq a+b+c+\frac{9}{a+b+c}\geq \frac{2}{3}+\frac{80}{3}=\frac{82}{3}$

Ta có đpcm.

Dấu "=" xảy ra khi $a=b=c=\frac{1}{9}$