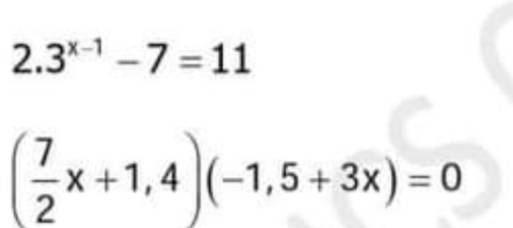`#3107.101107`
`2*3^(x - 1) - 7 = 11`
`=> 2*3^(x - 1) = 11 + 7`
`=> 2*3^(x - 1) = 18`
`=> 3^(x - 1) = 18 \div 2`
`=> 3^(x - 1) = 9`
`=> 3^(x - 1) = 3^2`
`=> x - 1 = 2`
`=> x = 2 + 1`
`=> x = 3`
Vậy, `x = 3`
_______
`(7/2x + 1,4)(-1,5 + 3x) = 0`
`=>`\(\left[{}\begin{matrix}\dfrac{7}{2}x+1,4=0\\-1,5+3x=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}\dfrac{7}{2}x=-1,4\\3x=1,5\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=-1,4\div\dfrac{7}{2}\\x=1,5\div3\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=-\dfrac{2}{5}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy, `x \in {-2/5; 1/2}.`
2.3ˣ⁻¹ - 7 = 11
2.3ˣ⁻¹ = 11 + 7
2.3ˣ⁻¹ = 18
3ˣ⁻¹ = 18 : 2
3ˣ⁻¹ = 9
3ˣ⁻¹ = 3²
x - 1 = 2
x = 3
------------
(7/2 x + 1,4)(-1,5 + 3x) = 0
7/2 x + 1,4 = 0 hoặc -1,5 + 3x = 0
*) 7/2 x + 1,4 = 0
7/2 x = -1,4
x = -1,4 : 7/2
x = -2/5
*) -1,5 + 3x = 0
3x = 1,5
x = 1,5 : 3
x = 1/2
Vậy x = -2/5; x = 1/2