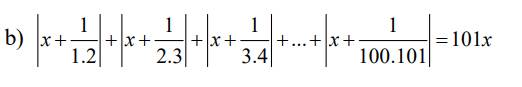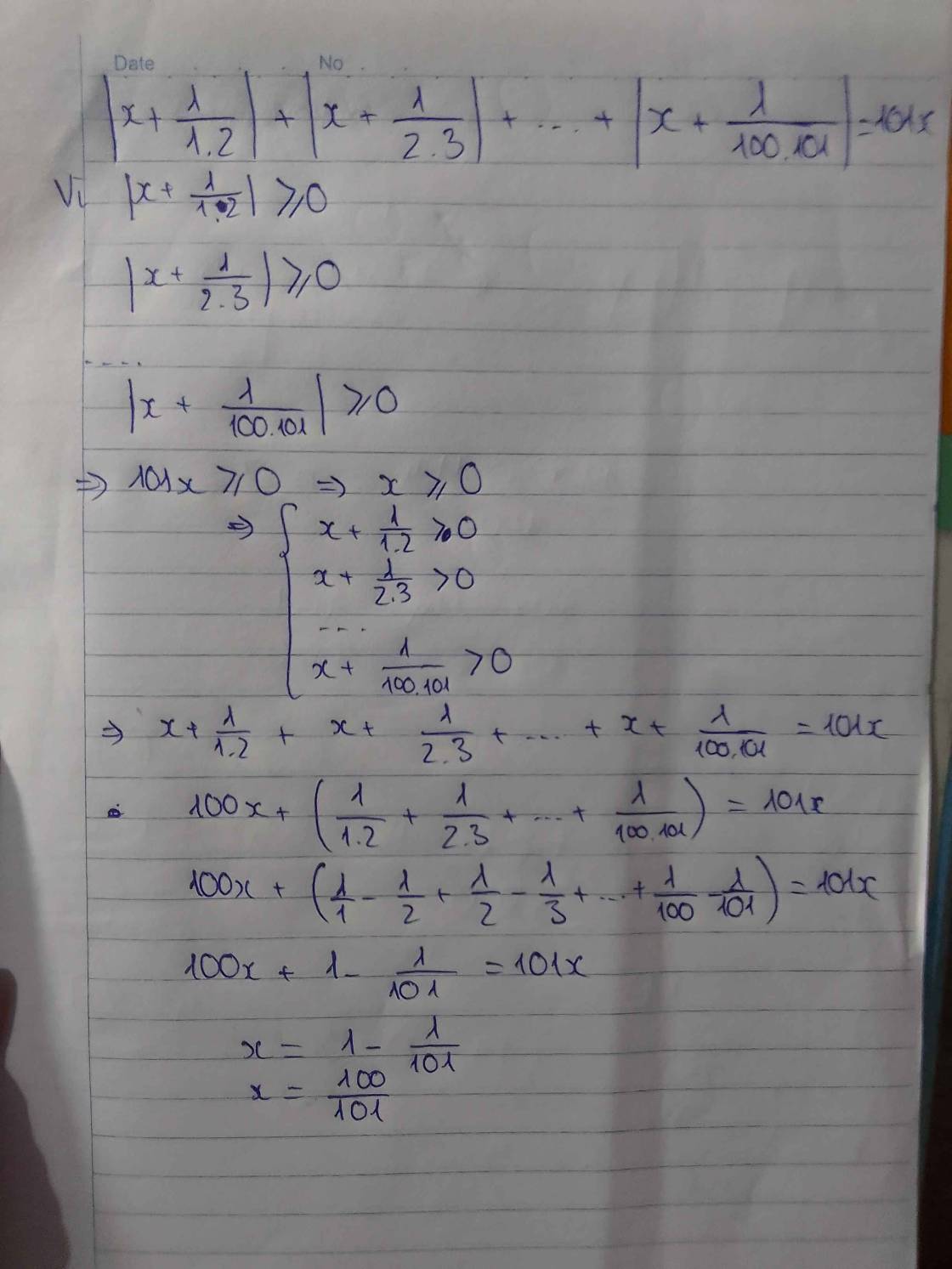\(\left|x+\dfrac{1}{1.2}\right|+\left|x+\dfrac{1}{2.3}\right|+\left|x+\dfrac{1}{3.4}\right|+...+\left|x+\dfrac{1}{100.101}\right|=101x\left(1\right)\)
Ta có :
\(\left|x+\dfrac{1}{1.2}\right|+\left|x+\dfrac{1}{2.3}\right|+\left|x+\dfrac{1}{3.4}\right|+...+\left|x+\dfrac{1}{100.101}\right|\ge x+\dfrac{1}{1.2}+x+\dfrac{1}{2.3}+x+\dfrac{1}{3.4}+...+x+\dfrac{1}{100.101}\)
\(\Rightarrow\left|x+\dfrac{1}{1.2}\right|+\left|x+\dfrac{1}{2.3}\right|+\left|x+\dfrac{1}{3.4}\right|+...+\left|x+\dfrac{1}{100.101}\right|\ge x+x+...+x\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{100.101}\)
\(\Rightarrow\left|x+\dfrac{1}{1.2}\right|+\left|x+\dfrac{1}{2.3}\right|+\left|x+\dfrac{1}{3.4}\right|+...+\left|x+\dfrac{1}{100.101}\right|\ge100x+1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}-\dfrac{1}{101}\)
\(\Rightarrow\left|x+\dfrac{1}{1.2}\right|+\left|x+\dfrac{1}{2.3}\right|+\left|x+\dfrac{1}{3.4}\right|+...+\left|x+\dfrac{1}{100.101}\right|\ge100x+1-\dfrac{1}{101}=100x+\dfrac{100}{101}\)
\(\left(1\right)\Rightarrow100x+\dfrac{100}{101}=101x\)
\(\Rightarrow x=\dfrac{100}{101}\)
Vậy nghiệm của \(\left(1\right)\) là \(x=\dfrac{100}{101}\)