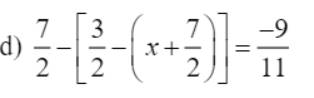\(\dfrac{7}{2}-\left[\dfrac{3}{2}-\left(x+\dfrac{7}{2}\right)\right]=\dfrac{-9}{11}\)
\(\Rightarrow\dfrac{7}{2}-\left(\dfrac{3}{2}-x-\dfrac{7}{2}\right)=\dfrac{-9}{11}\)
\(\Rightarrow\dfrac{7}{2}-\dfrac{3}{2}+x+\dfrac{7}{2}=\dfrac{-9}{11}\)
\(\Rightarrow\left(\dfrac{7}{2}-\dfrac{3}{2}+\dfrac{7}{2}\right)+x=\dfrac{-9}{11}\)
\(\Rightarrow\dfrac{7+7-3}{2}+x=\dfrac{-9}{11}\)
\(\Rightarrow\dfrac{11}{2}+x=\dfrac{-9}{11}\)
\(\Rightarrow x=\dfrac{-9}{11}-\dfrac{11}{2}\)
\(\Rightarrow x=\dfrac{-18}{22}-\dfrac{121}{22}\)
\(\Rightarrow x=\dfrac{-139}{22}\)
\(\dfrac{7}{2}\)-\(\left[\dfrac{3}{2}-\left(x+\dfrac{7}{2}\right)\right]\)=\(\dfrac{-9}{11}\)
⇒\(\dfrac{7}{2}\)-\(\left(\dfrac{3}{2}-x+\dfrac{7}{2}\right)\)=\(\dfrac{-9}{11}\)
⇒-(-2x-x)=\(\dfrac{-95}{22}\)
⇒x+2=\(\dfrac{-95}{22}\)
⇒x=\(\dfrac{-133}{22}\)