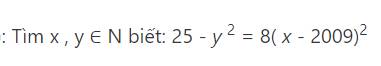Ta có :
\(25-y^2=8.\left(x-2009\right)^2\)
\(\Rightarrow25-8\left(x-2009\right)^2=y^2\)
Ta thấy VP của phương trình là một số chính phương vì y thuộc N.
\(\Rightarrow y^2\ge0\)
\(\Rightarrow25-8\left(x-2009\right)^2\ge0\)
\(\Rightarrow25\ge8\left(x-2009\right)^2\)
Vì : x thuộc N và \(8\left(x-2009\right)^2⋮8\)
\(\Rightarrow8\left(x-2009\right)^2\in\left\{0;16\right\}\)
Với \(8\left(x-2009\right)^2=0\Rightarrow x=2009\)
\(\Rightarrow\left[{}\begin{matrix}y=5\\y=-5\end{matrix}\right.\)
Với \(8\left(x-2009\right)^2=16\Rightarrow\left(x-2009\right)^2=2\)
TH này loại vì 2 không phải là một số chính phương .
Vậy..........
Trong quá trình mình làm nhiều chỗ mình lập luận chưa chuẩn thì mong bạn thông cảm.
Sửa:
Ta có : `8(x-2009)^2 >=0` và `vdots 8`.
`<=> 25-y^2>=0` và `vdots 8`
`<=> y=0/1/2/3/4/5 <=> 25-y^2=25/24/21/16/9/0` mà `25-y^2 vdots 8`
`<=> 25-y^2=24/16/0`.
`<=> y=+-1, +-3`
`y=+-1 => (x-2009)^2=3`
`<=> x=cancel O`.
`y=+-3 => (x-2009)^2=2`
`<=> x=cancel O`.
`y=+-5 => (x-2009)^2=0`
`<=> x=2009`.
Vậy `(x, y)=(+-5; 2009)`.
Ta có : `8(x-2009)^2 >=0` và `vdots 8`.
`<=> 25-y^2>=0` và `vdots 8`
`<=> y=0/1/2/3/4/5 <=> 25-y^2=25/24/21/16/9/0` mà `25-y^2 vdots 8`
`<=> 25-y^2=24/16`.
`<=> y=+-1, +-3`
`y=+-1 => (x-2009)^2=3`
`<=> x=cancel O`.
`y=+-3 => (x-2009)^2=2`
`<=> x=cancel O`.
Vậy ptr vô nghiệm.