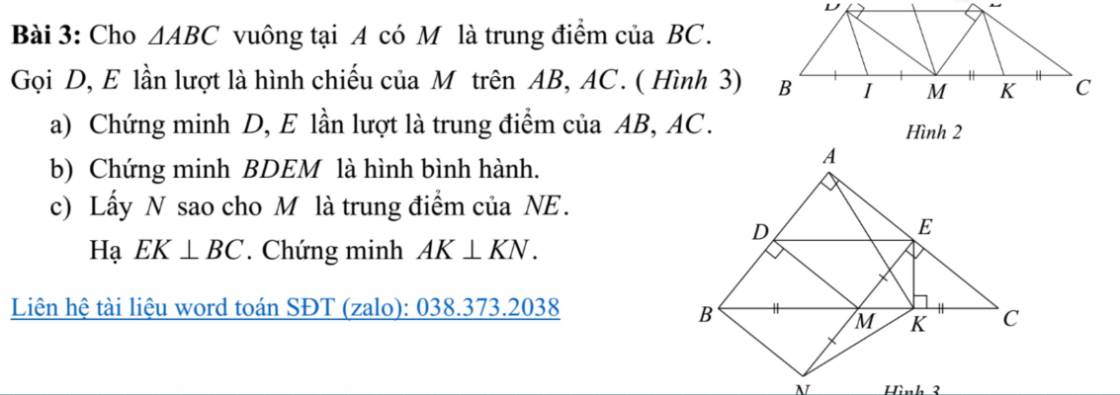
Bài 3:
a: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
b: Xét ΔABC có
M,E lần lượt là trung điểm của CB,CA
=>ME là đường trung bình của ΔABC
=>ME//AB và ME=AB/2
\(ME=\dfrac{AB}{2}\)
\(BD=\dfrac{AB}{2}\)
Do đó: ME=BD
ME//AB
\(D\in AB\)
Do đó: ME//BD
Xét tứ giác BDEM có
EM//BD
EM=BD
Do đó: BDEM là hình bình hành
c: \(EM=\dfrac{AB}{2}\)
\(EM=\dfrac{EN}{2}\)
Do đó: AB=EN
Xét tứ giác ABNE có
AB//NE
AB=NE
Do đó: ABNE là hình bình hành
Gọi O là giao điểm của AN và BE
Hình bình hành ABNE có \(\widehat{BAE}=90^0\)
nên ABNE là hình chữ nhật
=>AN cắt BE tại trung điểm của mỗi đường và AN=BE
=>O là trung điểm chung của AN và BE và AN=BE
\(AO=ON=\dfrac{AN}{2}\)
\(BO=EO=\dfrac{BE}{2}\)
mà AN=BE
nên AO=ON=EO=BO
ΔEKB vuông tại K
mà KO là đường trung tuyến
nên \(KO=\dfrac{EB}{2}\)
mà EB=AN
nên \(KO=\dfrac{AN}{2}\)
Xét ΔAKN có
KO là đường trung tuyến
\(KO=\dfrac{AN}{2}\)
Do đó: ΔAKN vuông tại K
=>AK\(\perp\)KN