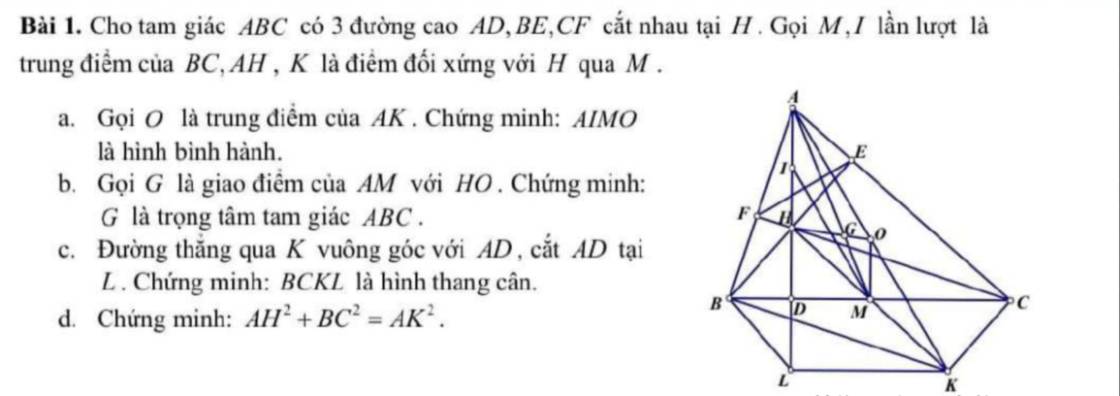
a: Xét ΔAHK có
M,O lần lượt là trung điểm của KH,KA
=>MO là đường trung bình của ΔAHK
=>MO//HA và \(MO=\dfrac{HA}{2}\)
MO//HA
\(I\in AH\)
Do đó: MO//AI và MO//HI
\(MO=\dfrac{HA}{2}\)
\(AI=HI=\dfrac{HA}{2}\)
Do đó: MO=AI=HI
Xét tứ giác AIMO có
OM//AI
OM=AI
Do đó: AIMO là hình bình hành
b: Xét ΔAHK có
AM,HO là các đường trung tuyến
AM cắt HO tại G
Do đó: G là trọng tâm của ΔAHK
=>\(AG=\dfrac{2}{3}AM\)
Xét ΔABC có
AM là đường trung tuyến
\(AG=\dfrac{2}{3}AM\)
Do đó: G là trọng tâm của ΔABC
c: Xét ΔHLK có
M là trung điểm của HK
MD//LK
Do đó: D là trung điểm của HL
Xét ΔCHL có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔCHL cân tại C
=>CH=CL
Xét tứ giác BHCK có
M là trung điểm chung của BC và HK
nên BHCK là hình bình hành
=>CH=BK
mà CH=CL
nên BK=CL
Xét tứ giác BCKL có BC//KL
nên BCKL là hình thang
Hình thang BCKL có BK=CL
nên BCKL là hình thang cân