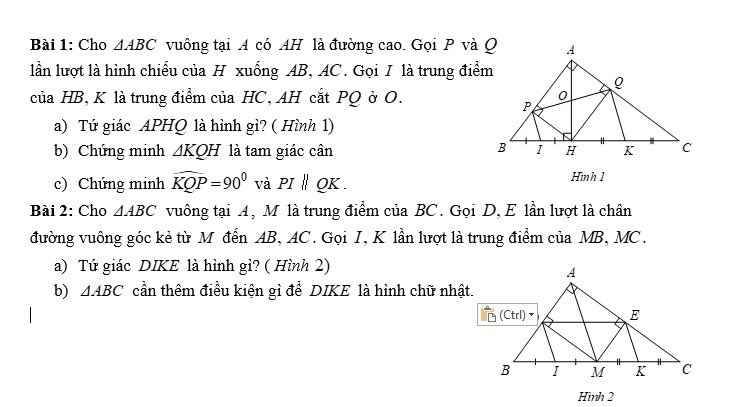
2:
a: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: Dlà trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
MC+MB=BC
=>2*MK+2*MI=BC
=>2*KI=BC
=>KI=BC/2(1)
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và \(DE=\dfrac{1}{2}BC\left(2\right)\)
Từ (1),(2) suy ra DE=KI
DE//BC
=>DE//KI
Xét tứ giác DEKI có
DE//KI
DE=KI
Do đó: DEKI là hình bình hành
b: Để DEKI là hình chữ nhật thì \(\widehat{DIK}=90^0\)
=>DI\(\perp\)MB
Xét ΔDMB có
DI là đường cao, là đường trung tuyến
=>ΔDMB cân tại D
=>\(\widehat{DMB}=\widehat{DBM}=\dfrac{180^0-\widehat{MDB}}{2}=45^0\)
=>\(\widehat{ABC}=45^0\)