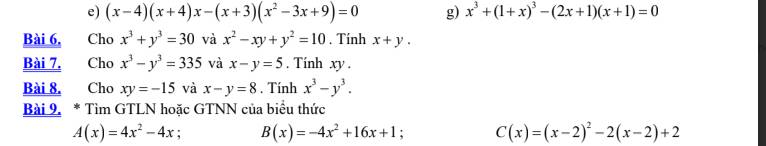Bài 6:
Theo hằng đẳng thức đáng nhớ thì:
$x^3+y^3=(x+y)(x^2-xy+y^2)$
$\Rightarrow 30=(x+y).10\Rightarrow x+y=3$
Bài 7:
Ta có:
$x^3-y^3=(x-y)^3+3xy(x-y)$
$\Rightarrow 335=5^3+3.xy.5$
$\Rightarrow 335=125+15xy$
$\Rightarrow xy=14$
Bài 8:
Ta có:
$x^3-y^3=(x^3-3x^2y+3xy^2-y^3)+(3x^2y-3xy^2)$
$=(x-y)^3+3xy(x-y)=8^3+3.(-15).8=152$
Bài 9:
$A(x)=4x^2-4x=(4x^2-4x+1)-1=(2x-1)^2-1$
Vì $(2x-1)^2\geq 0$ với mọi $x$
$\Rightarrow A(x)\geq 0-1=-1$
Vậy $A(x)_{\min}=-1$. Giá trị này đạt được khi $2x-1=0\Leftrightarrow x=\frac{1}{2}$
-----------------
$B(x)=-4x^2+16x+1$
$\Rightarrow -B(x)=4x^2-16x-1=(4x^2-16x+16)-17$
$=(2x-4)^2-17$
Vì $(2x-4)^2\geq 0$ với mọi $x$
$\Rightarrow -B(x)\geq 0-17=-17$
$\Rightarrow B(x)\leq 17$
Vậy $B(x)_{\max}=17$. Giá trị này được khi $2x-4=0\Leftrightarrow x=2$
-----------------
$C(x)=(x-2)^2-2(x-2)+2=(x-2)^2-2(x-2)+1+1=(x-2-1)^2+1=(x-3)^2+1$
Vì $(x-3)^2\geq 0$ với mọi $x$
$\Rightarrow C(x)\geq 0+1=1$
Vậy $C(x)_{\min}=1$. Giá trị này đạt tại $x-3=0\Leftrightarrow x=3$.
Bài 5:
e.
PT $\Leftrightarrow x(x^2-16)-(x^3+3^3)=0$
$\Leftrightarrow (x^3-16x)-(x^3+27)=0$
$\Leftrightarrow -16x-27=0$
$\Leftrightarrow x=\frac{-27}{16}$
g.
PT $\Leftrightarrow x^3+(x^3+3x^2+3x+1)-(2x^2+3x+1)=0$
$\Leftrightarrow 2x^3+3x^2+3x+1-2x^2-3x-1=0$
$\Leftrightarrow 2x^3+x^2=0$
$\Leftrightarrow x^2(2x+1)=0$
$\Leftrightarrow x^2=0$ hoặc $2x+1=0$
$\Leftrightarrow x=0$ hoặc $x=\frac{-1}{2}$