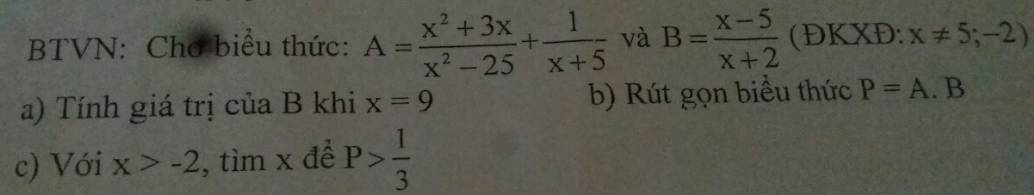\(a,B=\dfrac{x-5}{x+2}\left(ĐK:x\ne-2\right)\)
Thay \(x=9\) vào \(B\), ta được:
\(B=\dfrac{9-5}{9+2}=\dfrac{4}{11}\)
Vậy \(B=\dfrac{4}{11}\) khi \(x=9\).
\(b,P=A\cdot B=\left(\dfrac{x^2+3x}{x^2-25}+\dfrac{1}{x+5}\right)\cdot\dfrac{x-5}{x+2}\left(ĐK:x\ne\pm5;x\ne-2\right)\)
\(=\left[\dfrac{x^2+3x+x-5}{\left(x-5\right)\left(x+5\right)}\right]\cdot\dfrac{x-5}{x+2}\)
\(=\dfrac{x^2+4x-5}{\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x-5}{x+2}\)
\(=\dfrac{x^2+4x-5}{\left(x+5\right)\left(x+2\right)}\)
\(=\dfrac{x^2-x+5x-5}{\left(x+5\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x-1\right)+5\left(x-1\right)}{\left(x+5\right)\left(x+2\right)}\)
\(=\dfrac{\left(x-1\right)\left(x+5\right)}{\left(x+5\right)\left(x+2\right)}\)
\(=\dfrac{x-1}{x+2}\)
\(c,\) Để \(P>\dfrac{1}{3}\) với \(x>-2\)
thì \(\dfrac{x-1}{x+3}>\dfrac{1}{3}\)
\(\Rightarrow3x-3>x+3\)
\(\Rightarrow3x-x>3+3\)
\(\Rightarrow2x>6\)
\(\Rightarrow x>3\)
Kết hợp với điều kiện, ta được: \(x>3\)
#\(Toru☕\)