Bài 4:
a) \(\left(12x^4+4x^3-2x\right):2x\)
\(=2x\cdot\left(6x^3+2x^2-1\right):2x\)
\(=6x^3+2x^2-1\)
b) \(\left(2x-1\right)\left(3x^2+2x-5\right)\)
\(=2x\left(3x^2+2x-5\right)-\left(3x^2+2x-5\right)\)
\(=6x^3+4x^2-10x-3x^2-2x+5\)
\(=6x^3+x^2-12x+5\)
c) \(\left(15x^4+6x^3-9x\right):3x\)
\(=3x\cdot\left(5x^3+2x^2-3\right):3x\)
\(=5x^3+2x^2-3\)
d) \(\left(5x-1\right)\left(x^2+2x-6\right)\)
\(=5x\left(x^2+2x-6\right)-\left(x^2+2x-6\right)\)
\(=5x^3+10x^2-30x-x^2-2x+6\)
\(=5x^3+9x^2-32x+6\)
Bài 5:
(1)
a) \(A\left(x\right)+B\left(x\right)\)
\(=2x^2-x^3+3x+3+x^3-x^2-4-3x\)
\(=x^2-1\)
\(A\left(x\right)-B\left(x\right)\)
\(=2x^2-x^3+3x+3-x^3+x^2+4+3x\)
\(=3x^2-2x^3+6x+7\)
b) Ta có:
\(A\left(x\right)+B\left(x\right)=x^2-1\)
Mà: \(x^2-1=0\)
\(\Rightarrow x^2+x-x-1=0\)
\(\Rightarrow x\left(x+1\right)-\left(x+1\right)=0\)
\(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
(2)
a) \(A\left(x\right)+B\left(x\right)\)
\(=3x^2-2x^3+4x+1+2x^3-2x^2-5-4x\)
\(=x^2-4\)
\(A\left(x\right)-B\left(x\right)\)
\(=3x^2-2x^3+4x+1-2x^3+2x^2+5+4x\)
\(=5x^2-4x^3+8x+6\)
b) Ta có:
\(A\left(x\right)+B\left(x\right)=0\)
\(\Rightarrow x^2-4=0\)
\(\Rightarrow x^2-2x+2x-4=0\)
\(\Rightarrow x\left(x-2\right)+2\left(x-2\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Bài 1
a) P(x) = 5x⁵ - 7x² + 3x³ - 2x⁵ - 4x - 3x⁵
= (5x⁵ - 2x⁵ - 3x⁵) + 3x³ - 7x² - 4x
= 3x³ - 7x² - 4x
Q(x) x³ + 5x - 6 - 3x³
= (x³ - 3x³) + 5x - 6
= -2x³ + 5x - 6
b) P(x) + Q(x) = (3x³ - 7x² - 4x) + (-2x³ + 5x - 6)
= 3x³ - 7x² - 4x - 2x³ + 5x - 6
= (3x³ - 2x³) - 7x² + (-4x + 5x) - 6
= x³ - 7x² + x - 6
P(x) - Q(x) = (3x³ - 7x² - 4x) - (-2x³ + 5x - 6)
= 3x³ - 7x² - 4x + 2x³ - 5x + 6
= (3x³ + 2x³) - 7x² + (-4x - 5x) + 6
= 5x³ - 7x² - 9x + 6
c) P(0) = 3.0³ - 7.0² - 4.0 = 0
⇒ x = 0 là một nghiệm của P(x)
Q(0) = -2.0³ + 5.0 - 6 = -6
⇒ x = 0 không là nghiệm của Q(x)
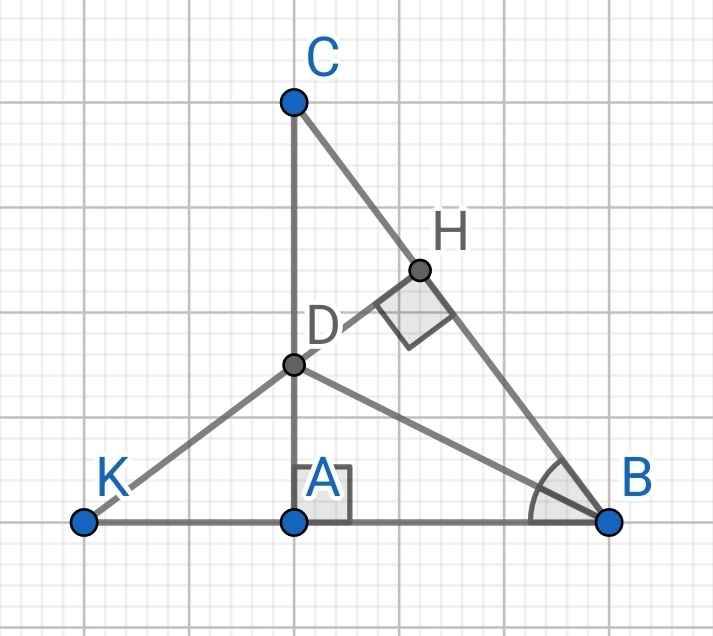a) Do BD là tia phân giác của ∆ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠HBD
Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD chung
∠ABD = ∠HBD (cmt)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
⇒ AD = HD (hai cạnh tương ứng)
b) ∆ADK vuông tại A
DK là cạnh huyền nên là cạnh lớn nhất
⇒ AD < DK
Mà AD = HD (cmt)
⇒ DH < DK
c) Xét hai tam giác vuông: ∆DAK và ∆DHC có:
AD = HD (cmt)
∠ADK = ∠HDC (đối đỉnh)
∆DAK = ∆DHC (cạnh góc vuông - góc nhọn kề)
⇒ AK = HC (hai cạnh tương ứng)
Do ∆ABD = ∆HBD (cmt)
⇒ AB = HB (hai cạnh tương ứng)
Mà AK = HC (cmt)
⇒ AB + AK = HB + HC
⇒ BK = BC
∆KBC có BK = BC (cmt)
⇒ ∆KBC cân tại B
3:
a: Xét ΔBAD vuông tại A và ΔBND vuông tại N có
BD chung
góc ABD=góc NBD
=>ΔBAD=ΔBND
b: ΔBAD=ΔBND
=>AD=DN
mà DN<DC
nên DA<DC
c: Xét ΔBKC có
KN,CA là đường cao
KN cắt CA tại D
=>D là trực tâm
=>BD vuông góc KC tại N
Xét ΔDAK vuông tại A và ΔDNC vuông tại N có
DA=DN
góc ADK=góc NDC
=>ΔDAK=ΔDNC
=>DK=DC
=>ΔDKC cân tại D
