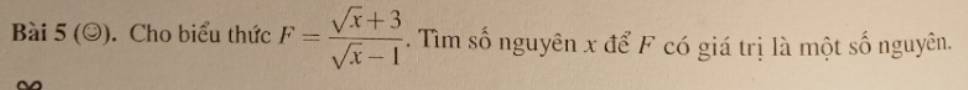ĐKXĐ: x>=0; x<>1
Để F là số nguyên thì \(\sqrt{x}-1+4⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{2;0;3;5\right\}\)
=>\(x\in\left\{4;0;9;25\right\}\)
Lơi giải:
$F=\frac{(\sqrt{x}-1)+4}{\sqrt{x}-1}=1+\frac{4}{\sqrt{x}-1}$
Để $F$ nguyên thì $\frac{4}{\sqrt{x}-1}$ nguyên.
Với $x$ nguyên thì điều này xảy ra khi $4\vdots \sqrt{x}-1$
$\Rightarrow \sqrt{x}-1\in\left\{\pm 1; \pm 2; \pm 4\right\}$
$\Rightarrow x\in\left\{0; 4; 9; 25\right\}$ (tm)