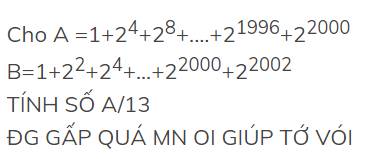Question

Answer 1

\(A=1+2^4+2^8+...+2^{2000}\)

\(2^4A=2^4\left(1+2^4+....+2^{2000}\right)\)

\(16A=2^4+2^8+2^{12}+...+2^{2004}\)

\(16A-A=\left(2^4+2^8+...+2^{2004}\right)-\left(1+2^4+2^8+...+2^{2000}\right)\)

\(15A=2^{2004}-1\)

\(A=\dfrac{2^{2004}-1}{15}\)

\(B=1+2^2+2^4+...+2^{2002}\)

\(2^2B=2^2\left(1+2^2+...+2^{2002}\right)\)

\(4B=2^2+2^4+...+2^{2004}\)

\(4B-B=\left(2^2+2^4+....+2^{2004}\right)-\left(1+2^2+2^4+...+2^{2002}\right)\)

\(3B=2^{2004}-1\)

\(B=\dfrac{2^{2004}-1}{3}\)

Sửa: \(\dfrac{A}{B}\)

\(=\dfrac{2^{2004}-1}{15}:\dfrac{2^{2004}-1}{3}\)

\(=\dfrac{2^{2004}-1}{15}\cdot\dfrac{3}{2^{2004}-1}\)

\(=\dfrac{3}{15}\)

\(=\dfrac{1}{5}\)