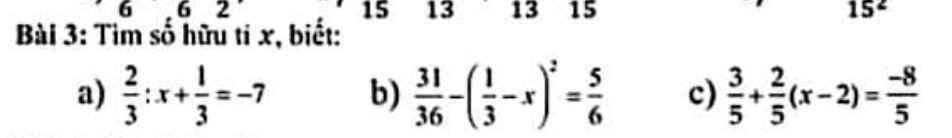a) \(\dfrac{2}{3}:x+\dfrac{1}{3}=-7\)
\(\dfrac{2}{3}:x=-7-\dfrac{1}{3}\)
\(\dfrac{2}{3}:x=-\dfrac{22}{3}\)
\(x=\dfrac{2}{3}:\left(-\dfrac{22}{3}\right)\)
\(x=-\dfrac{1}{11}\)
b) \(\dfrac{31}{16}-\left(\dfrac{1}{3}-x\right)^2=\dfrac{5}{6}\)
\(\left(\dfrac{1}{3}-x\right)^2=\dfrac{31}{36}-\dfrac{5}{6}\)
\(\left(\dfrac{1}{3}-x\right)^2=\dfrac{1}{36}\)
\(\Rightarrow\dfrac{1}{3}-x=\dfrac{1}{6}\) hoặc \(\dfrac{1}{3}-x=-\dfrac{1}{6}\)
*) \(\dfrac{1}{3}-x=\dfrac{1}{6}\)
\(x=\dfrac{1}{3}-\dfrac{1}{6}\)
\(x=\dfrac{1}{6}\)
*) \(\dfrac{1}{3}-x=-\dfrac{1}{6}\)
\(x=\dfrac{1}{3}-\left(-\dfrac{1}{6}\right)\)
\(x=\dfrac{1}{2}\)
Vậy \(x=\dfrac{1}{6};x=\dfrac{1}{2}\)
c) \(\dfrac{3}{5}+\dfrac{2}{5}\left(x-2\right)=-\dfrac{8}{5}\)
\(\dfrac{2}{5}\left(x-2\right)=-\dfrac{8}{5}-\dfrac{3}{5}\)
\(\dfrac{2}{5}\left(x-2\right)=-\dfrac{11}{5}\)
\(x-2=-\dfrac{11}{5}:\dfrac{2}{5}\)
\(x-2=-\dfrac{11}{2}\)
\(x=-\dfrac{11}{2}+2\)
\(x=-\dfrac{7}{2}\)
a) \(\dfrac{2}{3}:x+\dfrac{1}{3}=-7\)
\(\Rightarrow\dfrac{2}{3}:x=-7-\dfrac{1}{3}\)
\(\Rightarrow\dfrac{2}{3}:x=-\dfrac{22}{3}\)
\(\Rightarrow x=\dfrac{2}{3}:-\dfrac{22}{3}\)
\(\Rightarrow x=-\dfrac{1}{11}\)
b) \(\dfrac{31}{36}-\left(\dfrac{1}{3}-x\right)^2=\dfrac{5}{6}\)
\(\Rightarrow\left(\dfrac{1}{3}-x\right)^2=\dfrac{31}{36}-\dfrac{5}{6}\)
\(\Rightarrow\left(\dfrac{1}{3}-x\right)^2=\dfrac{1}{36}\)
\(\Rightarrow\left(\dfrac{1}{3}-x\right)^2=\left(\dfrac{1}{6}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{1}{3}-x=\dfrac{1}{6}\\\dfrac{1}{3}-x=-\dfrac{1}{6}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{6}\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\dfrac{2}{5}+\dfrac{2}{5}\left(x-2\right)=\dfrac{-8}{5}\)
\(\Rightarrow\dfrac{2}{5}\left(x-2\right)=\dfrac{-8}{5}-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{2}{5}\left(x-2\right)=-2\)
\(\Rightarrow x-2=-2:\dfrac{2}{5}\)
\(\Rightarrow x-2=-5\)
\(\Rightarrow x=-3\)