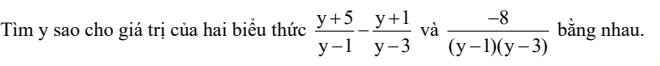ĐK: \(\left\{{}\begin{matrix}y\ne1\\y\ne3\end{matrix}\right.\)
Biểu thức trở thành: \(\dfrac{\left(y+5\right)\left(y-3\right)}{\left(y-1\right)\left(y-3\right)}-\dfrac{\left(y+1\right)\left(y-1\right)}{\left(y-1\right)\left(y-3\right)}=-\dfrac{8}{\left(y-1\right)\left(y-3\right)}\)
\(\Leftrightarrow\dfrac{y^2-3y+5y-15}{\left(y-1\right)\left(y-3\right)}-\dfrac{y^2-1}{\left(y-1\right)\left(y-3\right)}+\dfrac{8}{\left(y-1\right)\left(y-3\right)}=0\)
\(\Leftrightarrow y^2+2y-15-y^2+1+8=0\\ \Leftrightarrow2y=6\\ \Leftrightarrow y=\dfrac{6}{2}=3\left(loại\right)\)
Vậy không có giá trị y để hai biểu thức trên bằng nhau.
\(\dfrac{y+5}{y-1}-\dfrac{y+1}{y-3}=\dfrac{-8}{\left(y-1\right)\left(y-3\right)}\)
=>(y+5)(y-3)-y^2+1=-8
=>y^2+2y-15-y^2+1=-8
=>2y-14=-8
=>2y=6
=>y=3(loại)