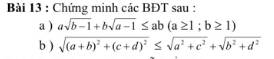Question

Answer 1

13a.

Áp dụng BĐT AM-GM:

$a\sqrt{b-1}=\sqrt{a^2(b-1)}=\sqrt{a(ab-a)}\leq \frac{a+ab-a}{2}=\frac{ab}{2}$
$b\sqrt{a-1}=\sqrt{b^2(a-1)}=\sqrt{b(ab-b)}\leq \frac{b+ab-b}{2}=\frac{ab}{2}$
Cộng theo vế 2 BĐT trên thu được:

$a\sqrt{b-1}+b\sqrt{a-1}\leq ab$ (đpcm)

Answer 2

13b.

BĐT cần cm tương đương với:

$(a+b)^2+(c+d)^2\leq a^2+c^2+b^2+d^2+2\sqrt{(a^2+c^2)(b^2+d^2)}$

$\Leftrightarrow a^2+b^2+c^2+d^2+2ab+2cd\leq a^2+c^2+b^2+d^2+2\sqrt{(a^2+c^2)(b^2+d^2)}$

$\Leftrightarrow ab+cd\leq \sqrt{(a^2+c^2)(b^2+d^2)}$

$\Leftrightarrow (ab+cd)^2\leq (a^2+c^2)(b^2+d^2)$

$\Leftrightarrow a^2b^2+c^2d^2+2abcd\leq a^2b^2+a^2d^2+b^2c^2+c^2d^2$

$\Leftrightarrow a^2d^2+b^2c^2-2abcd\geq 0$

$\Leftrightarrow (ad-bc)^2\geq 0$ (luôn đúng) 

Do đó ta có đpcm.