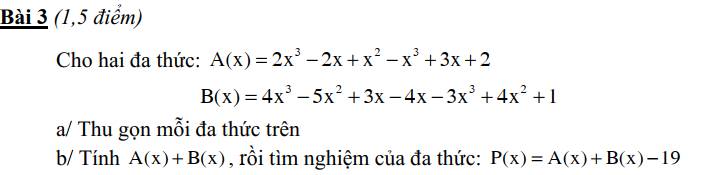\(a,\)
\(A\left(x\right)=2x^3-2x+x^2-x^3+3x+2\)
\(=\left(2x^3-x^3\right)+x^2+\left(-2x+3x\right)+2\)
\(=x^3+x^2+x+2\)
\(B\left(x\right)=4x^3-5x^2+3x-4x-3x^3+4x^2+1\)
\(=\left(4x^3-3x^3\right)+\left(-5x^2+4x^2\right)+\left(3x-4x\right)+1\)
\(=x^3-x^2-x+1\)
\(b,A\left(x\right)+B\left(x\right)=\left(x^3+x^2+x+2\right)+\left(x^3-x^2-x+1\right)\)
\(=x^3+x^2+x+2+x^3-x^2-x+1\)
\(=2x^3+3\)
Ta có : \(A\left(x\right)+B\left(x\right)=19\)
\(\Rightarrow2x^3+3=19\)
\(\Rightarrow2x^3=16\)
\(\Rightarrow x^3=8\)
\(\Rightarrow x=2\)
Vậy nghiệm của \(P\left(x\right)\) là \(x=2\)
a)Ta có:
\(A\left(x\right)=2x^3-2x+x^2-x^3+3x+2\)
\(=\left(2x^3-x^3\right)+\left(3x-2x\right)+x^2+2\)
\(=x^3+x+x^2+2\)
\(=x^3+x^2+x+2\)
\(B\left(x\right)=4x^3-5x^2+3x-4x-3x^3+4x^2+1\)
\(=\left(4x^3-3x^3\right)+\left(4x^2-5x^2\right)+\left(3x-4x\right)+1\)
\(=x^3-x^2-x+1\)
b) Ta có:
\(A\left(x\right)+B\left(x\right)=x^3+x^2+x+2+x^3-x^2-x+1\)
\(=\left(x^3+x^3\right)+\left(x^2-x^2\right)+\left(x-x\right)+\left(2+1\right)\)
\(=2x^3+3\)
Do đó:
\(2x^3+3=19\)
\(\Rightarrow2x^3=16\)
\(\Rightarrow x^3=8\)
\(\Rightarrow x=2\)
\(\Rightarrow\)Nghiệm của đa thức P(x) là 2