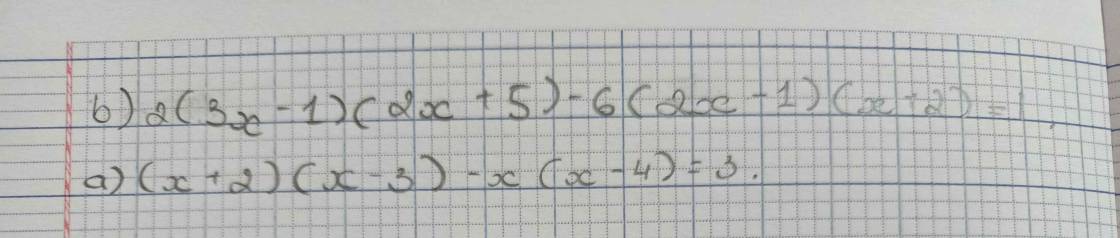`b)`
\(2\left(3x-1\right)\left(2x+5\right)-6\left(2x-1\right)\left(x+2\right)=1\\ \left(6x-2\right)\left(2x+5\right)-\left(12x-6\right)\left(x+2\right)=1\\ 2x\cdot\left(6x-2\right)+5\left(6x-2\right)-x\left(12x-6\right)-2\left(12x-6\right)=1\\ 12x^2-4x+30x-10-12x^2+6x-24x+12=1\\ \left(12x^2-12x^2\right)-\left(4x-3x-6x+24x\right)-\left(10-12\right)=1\\ 19x+2=1\\ 19x=-1\\ x=-\dfrac{1}{19}\)
`c)`
\(\left(x+2\right)\left(x-3\right)-x\left(x-4\right)=3\\ x\cdot\left(x-3\right)+2\cdot\left(x-3\right)-x^2+4x=3\\ x^2-3x+2x-6-x^2+4x=3\\ \left(x^2-x^2\right)-\left(3x-2x+x-4x\right)-6=3\\ 2x-6=3\\ 2x=9\\ x=\dfrac{9}{2}\)
b)\(2\left(3x-1\right)\left(2x+5\right)-6\left(2x-1\right)\left(x+2\right)=1\)
⇔\(2\left(6x^2+15x-2x-5\right)-6\left(2x^2+4x-x-2\right)=1\)
⇔\(12x^2+30x-4x-10-12x^2-24x+6x+12=1\)
⇔\(12x^2+30x-4x-12x^2-24x+6x=1+10-12\)
⇔\(18x=-1\)
⇔\(\dfrac{8x}{8}=\dfrac{-1}{8}\)
⇔\(x=-\dfrac{1}{8}\)
a)\(\left(x+2\right)\left(x-3\right)-x\left(x-4\right)=3\)
⇔\(x^2-3x+2x-6-x^2+4x=3\)
⇔\(x^2-3x+2x-x^2+4x=3+6\)
⇔\(3x=9\)
⇔\(\dfrac{3x}{3}=\dfrac{9}{3}\)
⇔\(x=3\)