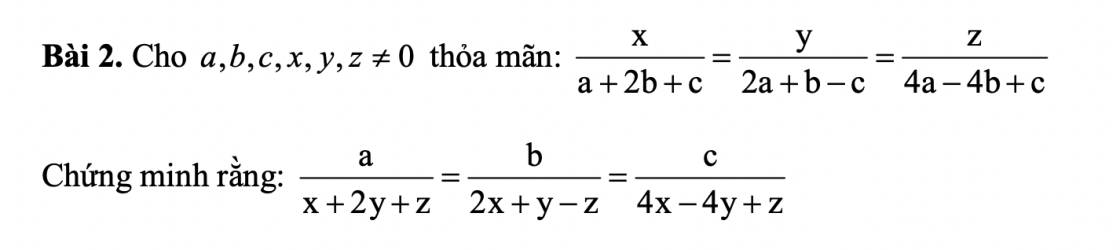Question

Answer 1

Đặt \(\dfrac{x}{a+2b+c}=\dfrac{y}{2a+b-c}=\dfrac{z}{4a-4b+c}=k\)

=>x=ka+2kb+kc; y=2ak+bk-ck; z=4ka-4kb+kc

=>x+2y+z=9ka

=>\(\dfrac{a}{x+2y+z}=\dfrac{1}{9k}\)

Lại có: \(\left\{{}\begin{matrix}x=ka+2kb+kc\\y=2ka+kb-kc\\z=4ka-4kb+kc\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=2ka+4kb+2kc\\y=2ka+kb-kc\\z=4ka-4kb+kc\end{matrix}\right.\)

=>2x+y-z=9bk

=>b/2x+y-z=1/9k

Chứng minh tương tự, ta được: c/4x-4y+z=1/9k

=>ĐPCM