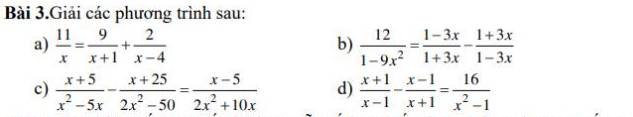a: \(\Leftrightarrow\dfrac{11\left(x+1\right)\left(x-4\right)}{x\left(x+1\right)\left(x-4\right)}=\dfrac{9x\left(x-4\right)}{x\left(x+1\right)\left(x-4\right)}+\dfrac{2x\left(x+1\right)}{x\left(x+1\right)\left(x-4\right)}\)
=>11(x^2-3x-4)=9x^2-36x+2x^2+2x
=>11x^2-33x-44=11x^2-34x
=>x=44
b: \(\Leftrightarrow\dfrac{-12}{\left(3x-1\right)\left(3x+1\right)}=-\dfrac{3x-1}{3x+1}+\dfrac{3x+1}{3x-1}\)
=>-(3x-1)^2+(3x+1)^2=-12
=>-9x^2+6x-1+9x^2+6x+1=-12
=>12x=-12
=>x=-1
c: =>\(\dfrac{x+5}{x\left(x-5\right)}-\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{2x\left(x+5\right)}\)
=>\(2\left(x+5\right)^2-x\left(x+25\right)=\left(x-5\right)^2\)
=>2x^2+20x+50-x^2-25x=x^2-10x+25
=>x^2-5x+50=x^2-10x+25
=>5x=-25
=>x=-5(loại)
d: =>(x+1)^2-(x-1)^2=16
=>x^2+2x+1-x^2+2x-1=16
=>4x=16
=>x=4
d. \(\dfrac{x+1}{x-1}\) - \(\dfrac{x-1}{x+1}\) = \(\dfrac{16}{x^2-1}\)
<=> \(\dfrac{x+1}{x-1}\) - \(\dfrac{x-1}{x+1}\) = \(\dfrac{16}{\left(x-1\right)\left(x+1\right)}\) (1)
ĐKXĐ <=> x - 1 \(\ne\) 0 <=> x \(\ne\) 1
x + 1 \(\ne\) 0 <=> x \(\ne\) -1
(1) <=> \(\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\) - \(\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\) = \(\dfrac{16}{\left(x-1\right)\left(x+1\right)}\)
=> (x + 1)(x+1) - (x -1)(x-1) = 16
=> x2 + x + x +1 + x2 - x - x + 1 = 16
=>x2 + x + x +1 + x2 - x - x + 1 - 16 = 0
=> 2x2 - 14 = 0
=> 2x(x - 7) = 0
=> 2x =0
x - 7 = 0
=> x = 0(n)
x = 7(n)